如何設計一求二正整數最大公因數的程式

範例執行程式

• 疊代程式

• 遞迴程式

步驟一：如何手動計算：輾轉相除法 (Eucledean method) 如下圖：

1. 以較大的數 (75) 為被除數， 較小的數 (42) 為除數， 75 / 42 = 1 餘 33

2. 以前一步驟的除數為被除數， 餘數為除數， 42 / 33 = 1 餘 9

3. 33 / 9 = 3 餘 6

4. 9 / 6 = 1 餘 3

5. 6 / 3 = 2 餘 0 , 除數 3 即可為最大公因數

步驟二：以疊代 (Iterative) 方式設計程式

轉換上述手動動作

1. 第一數為 75，第二數為 42
   可以轉換為下列程式：
   iFirstNumber = 75; iSecondNumber = 42;

2. 75 / 42 商為 1 餘 33
   可以轉換為下列程式：
   iQuotient = iFirstNumber / iSecondNumber; iRemainder = iFirstNumber % iSecondNumber;

3. 42 / 33 商為 1 餘 9
   在前面一個步驟中 42 是放在 iSecondNumber 之中， 33 是除出來的餘數， 放在 iRemainder 之中， 因此可以轉換為下列程式：
   iQuotient = iSecondNumber / iRemainder; iRemainder = iSecondNumber % iRemainder;

4. 33 / 9 商為 3 餘 6
   同樣地，可以轉換為下列程式：
   iQuotient = iRemainder / iRemainder; iRemainder = iRemainder % iRemainder;

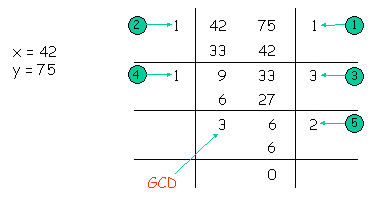
   哇! 不對了， 這裡的被除數 iRemainder 是前一步驟中的除數， 這裡的除數 iRemainder 是前一步驟中的餘數， 可是在產生餘數時我們把除數給蓋掉了。

   在前一步驟中

   iRemainder = iSecondNumber % iRemainder;
   之前我們必須先將先前的餘數記錄下來，例如：
   iDivident = iRemainder;

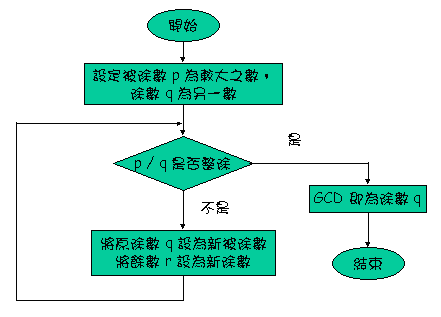
   還有另外一個問題是： 每一次做除法時除數和被除數放的地方 (變數) 都不一樣， 這樣子寫程式時很不方便， 也沒有辦法用迴圈來處理， 因為迴圈內所作的事情除了變數內的資料值不一樣之外， 動作應該要是一樣的。

1. 第一數為 75，第二數為 42
   可以轉換為下列程式：
   iFirstNumber = 75; iSecondNumber = 42;

2. 75 / 42 商為 1 餘 33
   可以轉換為下列程式：
   iDivident = iFirstNumber; iDivisor = iSecondNumber; iQuotient = iDivident / iDivisor; iRemainder = iDivident % iDivisor;

3. 42 / 33 商為 1 餘 9
   可以轉換為下列程式：
   iDivident = iSecondNumber; iDivisor = iRemainder; iQuotient = iDivident / iDivisor; iRemainder = iDivident % iDivisor;

4. 33 / 9 商為 3 餘 6
   可以轉換為下列程式：
   iDivident = iDivisor; iDivisor = iRemainder; iQuotient = iDivident / iDivisor; iRemainder = iDivident % iDivisor;

5. 9 / 6 商為 1 餘 3
   可以轉換為下列程式：
   iDivident = iDivisor; iDivisor = iRemainder; iQuotient = iDivident / iDivisor; iRemainder = iDivident % iDivisor;

6. 6 / 3 商為 2 餘 0 , 除數 3 即可為最大公因數
   可以轉換為下列程式：
   iDivident = iDivisor; iDivisor = iRemainder; iQuotient = iDivident / iDivisor; iRemainder = iDivident % iDivisor; if (iRemainder == 0) { iGCD = iDivisor; stop the program }

設計資料變數

1. 被除數 int iDividend
2. 除數 int iDivisor
3. 第一數 int iFirstNumber
4. 第二數 int iSecondNumber
5. 商數 int iQuotient
6. 餘數 int iRemainder
7. 最大公因數 int iGCD

安排基本流程

步驟三：程式各部分測試

1. 比較兩數的大小來決定誰要除以誰
   if (iFirstNumber == iSecondNumber) { iGCD = iFirstNumber; printf("The GCD of %d and %d is %d\n", iFirstNumber, iSecondNumber, iGCD); return; } else if (iFirstNumber > iSecondNumber) { iDividend = iFirstNumber; iDivisor = iSecondNumber; } else { iDividend = iSecondNumber; iDivisor = iFirstNumber; }

2. label: iRemainder = iDividend % iDivisor; if (iRemainder == 0) { iGCD = iDivisor; printf("The GCD of %d and %d is %d\n", iFirstNumber, iSecondNumber, iGCD); return; } else { iDividend = iDivisor; iDivisor = iRemainder; } goto label;

3. 我們禁止大家使用上面的 goto 敘述， 讓我們用 while 敘述來改寫一下：
   iRemainder = iDividend % iDivisor; while (iRemainder != 0) { iDividend = iDivisor; iDivisor = iRemainder; iRemainder = iDividend % iDivisor; } iGCD = iDivisor; printf("The GCD of %d and %d is %d\n", iFirstNumber, iSecondNumber, iGCD); return;

4. 再變換一下指令順序， 可以不必重覆寫兩次 iDividend % iDivisor：
   while ((iRemainder=iDividend%iDivisor) != 0) { iDividend = iDivisor; iDivisor = iRemainder; } iGCD = iDivisor; printf("The GCD of %d and %d is %d\n", iFirstNumber, iSecondNumber, iGCD); return;

步驟四：測試

1. 30 48 -> 6
2. 656243 49952070 -> 1687

步驟五：以遞迴 (recursive) 方式製作程式

只要求出 42 及 33 的最大公因數， 就可以輕鬆地得到 75 及 42 的最大公因數。

int findGCD(int iDivident, int iDivisor) { int iRemainder = iDivident % iDivisor; if (iRemainder == 0) return iDivisor; else return findGCD(iDivisor, iRemainder); }

回 程式設計課程 首頁
by Pei-yih Ting
E-mail: pyting@cs.ntou.edu.tw