以平方再乘法計算指數

這個程式是要你算出 xⁿ 的數值出來

xⁿ 應該是大家都會算的東西， 而且我們只要求 n 是一個正整數， 那麼最簡單的辦法就是把 x 連續乘 n 遍啦! 當然這種作法所需要的乘法有一點多， 如果是 2.5⁶⁵⁵³⁶ 的話， 你只要乘 65536 次就好了；

好一點的作法可以把 n 做一個因式分解的動作， 然後乘法的次數可以降低下來， 上例中， 65536 = 2¹⁶， 所以我們可以先做 2.5²， 然後再做 6.25¹⁶， 一下子降低很多乘法次數了吧! 可是要做因式分解耶， 會不會增加更多的運算啊? 會不會太複雜了啊， 還有質數麼辦呢?

下面我們要介紹的平方再乘法是一個很常用的方法， 可以很快地算出一個數的次方， 而且乘法運算的次數在一定的次數以下：

如果你將 n 用二進位表示法表示為

n = (n_m-1 n_m-2 ... n₀)₂ 　n_i 為 0 或是 1

n = n₀ + 2 * (n₁ + 2 * (n₂ + 2 * ( ... + 2 * n_m-1)...))

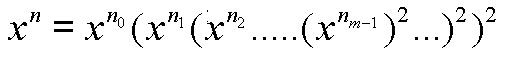
像上面這樣子如果 n 可以用 32 位元表示的話， 最多需要 63 次乘法就可以完成 xⁿ 的運算， 當然你要想想看 x 做那麼多次方的數字是不是已經沒有辦法在計算機內表示了呢?

怎樣寫一個 C 程式來完成上面的運算呢?

1. 首先解決關鍵的運算部份：

   你可以把 n 連續除以 2 來求出 n 的二進位表示法， 並且用陣列變數來記錄 n 的二進位表示法

   也可以直接用 n & (1L << i) 的方式來測試第 i 個位元是否為 1

2. 要完成上面的 "平方再乘法" 現在就比較容易了：

   你應該要先設定一個變數 y 為 1， 寫一個迴圈從 MSB n_m-1 開始檢查， 如果發現該位元是 1 時乘上 x， 如果是 0 的話就不要乘任何數， 然後做平方的動作， 然後依序檢查第 m-2 個位元， 第 m-3 個位元， ..... 如此繼續下去直到 n₁， 對於 LSB n₀ 則只要決定是否乘上 x 就可以了。

程式要求

1. 由於次方很多的時候很容易造成溢位， 請測試看看你的程式能夠偵測出這種狀況嗎?

2. 請在程式內加一段對照的程式， 用直接乘 n 次的方法來算出同樣的 xⁿ

3. 請在程式內再加一段對照的程式， 直接用 math.h 函式庫中的 pow(x, n) 函式算出同樣的 xⁿ

4. 請儘量用函式來簡化程式的邏輯

5. 請以 ANSI C 語法及函式庫來製作

範例執行程式

回 程式設計課程 首頁

製作日期: 99/10/19 by 丁培毅 (Pei-yih Ting)
E-mail: pyting@cs.ntou.edu.tw