以 Riemann Sum 求函式之定積分的近似值

我們想要計算的函式如下
| 5 4 3 2 |
f(x) = | a x + a x + a x + a x + a x + a |
| 5 4 3 2 1 0 |
上式中||代表絕對值
請計算 f(x) 由 a 積分至 b 的結果
也就是在函式 f(x) 與 X-座標軸 [a,b] 之間的面積
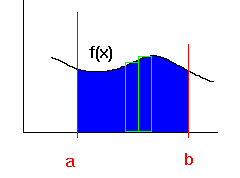
a, b, 以及所有的係數都是使用者輸入的,
例如:a = -5, b = 5, a5 = 6, a4 = 5, a3 = 4, a2 = 3,
a1 = 2, a0 = 1
Riemann Sum
簡單的說就是用多個小塊長方形的面積和來近似積分的值
該近似到什麼地步呢?
如果有誤差的話,
理想上應該是要近似到一個百分比的誤差以內才對。
假設使用者要求近似到百分之一,
那麼也就是說如果正確的積分值是 100 的話,
我們求得的近似值誤差應該要不能超過百分之一,
或是說近似值應該在 99 到 101 之間。

該怎樣製作這個程式呢?
-
要使用 Riemann Sum 來近似這個定積分的話,
首先我們必須要讓程式能夠將函式與 X
軸間的面積分成一小塊一小塊地計算出來,
每一塊長方形的面積當然是長與寬的乘積,
如果我們可以將 X 軸上 a 到 b 等分成 N 等分,
寬就是 (b-a)/N,
至於長度的話就必須讓程式求出 f((a+b)/2) 的數值了。
-
到底 N 該用多大呢?
這應該和函式 f 在積分區域間變化的情形有關係,
在這裡我們不用去研究這個關係,
最簡單的方式就是讓使用者直接輸入一個數字就是了,
比較好一點的程式可以用嘗試錯誤的方法來做,
也就是你可以由一個適當的數值開始,
然後慢慢地增加 N 的數值,
如果程式發現 N 增加的時候 Riemann Sum 不太改變的話,
我們就可以結束這個程式了。
-
那怎樣才知道 Riemann Sum 不太改變了呢?
假設我們用 N = 400 時算出來的和是 101,
用 N = 401 時算出來的和是 100.5,
改變的比例是 (100-100.5)/100.5,
這個比例越低的話就表示 N 繼續增大時結果不太改變了,
也就可以不要再增加 N 了,
所以我們可以要求使用者輸入一個比例
(例如 0.01 ) 來限制程式測試執行的次數,
當改變的比例低於這個數字的時候就不要再增加 N 的數值了。

程式要求
-
係數請以陣列變數存放
-
數學函式 f(.) 請一定要用 C 的函式來撰寫,
在 main() 函式內讀到的係數請以參數的方式傳進函式內執行
-
你可以只讓使用者輸入一個 N 的數值範圍來執行這個程式,
(如果有時間的話,
請你進一步撰寫自動決定 N 的數值的程式,
在這種情況下,
針對某一個 N 的數值來計算 Riemann Sum 這個動作也請你寫成一個 C 函式)
-
請以 ANSI C 語法及函式庫來製作

範例執行程式
直接輸入 N 值範圍的範例
請測試
-
Please input 6 coefficients (a0 a1 a2 a3 a4 a5): 1 2 0 0 0 0
Please input minimal N and maximal N value: 1 10 1
Please input integration range a and b: 1 20
-
Please input 6 coefficients (a0 a1 a2 a3 a4 a5): 1 2 3 4 5 6
Please input minimal N and maximal N value: 10 200 10
Please input integration range a and b: -1 1
-
Please input 6 coefficients (a0 a1 a2 a3 a4 a5): 0 1 0 0 0 0
Please input minimal N and maximal N value: 40 60 1
Please input integration range a and b: -1 1
自動決定 N 值的範例




![]()
![]()
![]()

