解一元二次方程式的根?

一元二次方程式

步驟一:如何動手去算
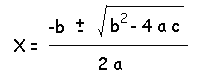
-
測試是否有虛根
-
若是小於 0 則
-
若是等於 0 則
-
若是大於 0 則

步驟二:安排基本流程
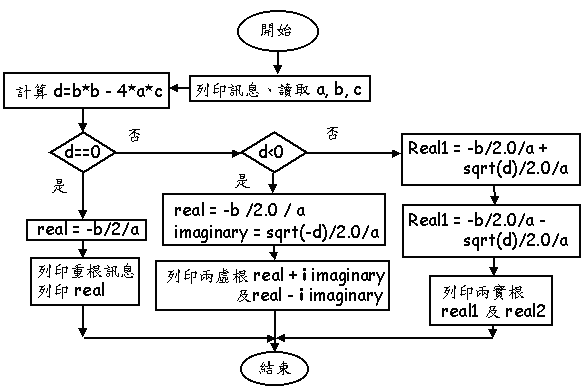

設計資料變數
方程式係數 double coefA, coefB, coefC;
判別式 double determinant;
實部虛部 double readPart, imaginaryPart;
重根 double realDuplicate;
兩實根 double read1, real2;

步驟三:程式各部分語法
-
determinant = coefB*coefB - 4.0*coefA*coefC;
-
if (determinant == 0)
{
...
}
else if (determinant < 0)
{
...
}
else /* if (determinant > 0) */
{
...
}
-
realDuplicate = -coefB / 2.0 / coefA;
realPart = -coefB / 2.0 / coefA;
#include <math.h>
imaginaryPart = sqrt(-determinant) / 2.0 / coefA;
real1 = -coefB / 2.0 / coefA + sqrt(determinant) / 2.0 / coefA;
real2 = -coefB / 2.0 / coefA - sqrt(determinant) / 2.0 / coefA;
-
#include <stdio.h>
printf("此程式可計算一元二次方程式的根\n");
printf("請輸入 ax^2 + bx + c = 0 之三個係數");
scanf("%lf%lf%lf", &coefA, &coefB, &coefC);
printf("一元二次方程式 %lfx^2 + %lfx + %lf = 0 之根為:\n", coefA, coefB, coefC);
printf("兩相同實數:%lf\n", readDuplicate);
printf("兩虛根:%lf + i%lf 及 %lf -i%lf\n", readPart, imaginaryPart, readPart, imaginarypart);
printf("兩實數:%lf 及 %lf\n", real1, real2);

注意一:
計算兩相異實根時可以用
double tmp1, tmp2, tmp3;
tmp1 = 2.0 * coefA;
tmp2 = -coefB / tmp1;
tmp3 = sqrt(determinant) / tmp1;
real1 = tmp2 + tmp3;
real2 = tmp2 - tmp3;
其中 tmp1, tmp2, tmp3 為暫時的變數,
如此一來程式裡就不會重覆寫兩次
coefB / 2.0 / coefA 了,
當然也可以不必重覆計算兩次,
似乎是利多於弊的寫法。
可是這樣子卻犧牲了可讀性,
看到 real1 及 real2 時你還需要再多花一些時間
才能了解到它們就是 -b + √(b^2 -4ac) 及 -b - √(b^2 -4ac) ,
現在的編譯器加上一些選項以後其實可以自動將第一段程式轉為第二段程式,
在執行時一點都不會浪費 CPU 時間,
因此你在撰寫程式時要常常去評估
這類可讀性與計算效率的問題,
視應用領域的不同甚至兩者會有不同的比重,
例如在科學運算的領域中計算效率的比重較高,
在系統軟體中可讀性的比重較高。

注意二:
在上面的程式裡大家一定還有一點覺得很疑惑的:
在三種情形下為何不只用兩個變數 x1, x2 即可,
為什麼要用
realDuplicate, realPart, imaginaryPart, real1 和 real2,
是不是有點浪費呢?
其實這還是可讀性的問題,
如果你寫成
if (determinant == 0)
{
x1 = -coefB / 2.0 / coefA;
printf(.....);
}
else if (determinant < 0)
{
x1 = -coefB / 2.0 / coefA;
x2 = sqrt(-determinant) / 2.0 / coefA;
printf(.....);
}
else
{
x1 = -coefB / 2.0 / coefA + sqrt(determinant) / 2.0 / coefA;
x2 = -coefB / 2.0 / coefA - sqrt(determinant) / 2.0 / coefA;
printf(.....);
}
其實這三部分中的 x1, x2 是相互無關的,
但是因為共用一個變數,
讀程式的人必須完全看懂你的程式邏輯後,
才能知道原來各自跑各自的根本沒有關聯,
這樣子寫程式很容易增加程式的複雜度耶!
記住好的習慣可以降低程式的複雜度。



![]()
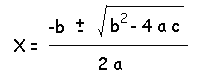
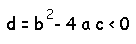
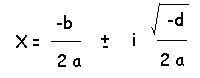
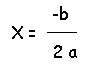
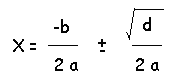
![]()

![]()
![]()
![]()
![]()
