

每一個 C 程式都是由函式組成的, 由 main() 函式開始執行, main() 函式處理整個問題, 為了降低程式的複雜度, 通常將問題依其特性分解為許多部份, main() 函式呼叫許多獨立的函式來解決個別的問題, 一層一層地分工合作下去。 因此函式呼叫其它函式是理所當然的, 但是呼叫自己會不會有些矛盾呢?
![]()
這個要求可以用一個簡易的 for 迴圈來達成
換一種說法也就是說當 CPU 呼叫 sum(10), sum(10) 這個函式在執行時, 會重複地呼叫 sum() 函式九次, 連同前面 sum(10) 的呼叫總共有 10 次之多, 而且這十次函式呼叫沒有一次能夠自己獨自完成, 每一次函式呼叫時參數變數 n 內的數值也是不一樣的, 依次為 10、9、8、7、6、5、4、3、2、1, 在同樣的一個函式中使用同樣的一個變數? 那麼後來的數字會不會蓋掉前面的數字呢? 本來在 sum() 函式處理參數 n 為 10 的呼叫時, 會執行 sum(9) + n 的動作, 當然此時 n 內的數值應該要是 10 才會正確地工作, 但是在進行 sum(9) 的呼叫時變數 n 內的數值會不會被改為 9 呢?
上面問題的答案是不會。
簡單地說, 每一次 CPU 在執行一個函式時, 都必須替所有的參數及區域變數準備新的儲存空間, 如此就算一個函式被呼叫好多次, 在每次呼叫時其內的變數和其它次呼叫時的變數是完全不同、 不互相影響的, 細節請參考函式呼叫時堆疊的使用。
![]()
沒錯, 運作時比較複雜, 但是函式設計及製作時應該是比較簡單的, 比較上面同樣功能函式的兩個版本, 以疊代方式製作的函式中, 程式設計者腦中必須能夠掌握在運作時變數內資料內容的變化, 迴圈重覆的次數愈多時程式設計者腦中要掌握的變化就愈多; 反之以遞迴方式製作的函式中, 程式設計者腦中需要先假設當問題的規模縮小一點時是可以用某一函式解決的, 例如:
求 sum(10) 時可以假設 sum(9) 是可以用其它的函式求出來的,
若有此 sum(9) 的話, 要如何求得 sum(10) 的結果則是此函式內需要專注來處理的, 也就是 sum(10) = sum(9) + 10, 一般化之後就是 sum(n) = sum(n-1) + n, 如此函式的主體就已經順利完成了。 觀念上是不是比較簡單呢?
![]()
等等。
如果你熟悉數學歸納法的話, 一定會覺得前面的例子似曾相識, 而且簡直就是利用標準的數學歸納法來得到的, 沒錯, 在前面連加的例子裡的確是這樣子的。 不過一般來說, 遞迴演算法是一種用程式來實現 Divide and Conquer 策略的重要方法。
所謂的 Divide and Conquer 是我們常常用來解決問題的一種策略, 就是將一個大的問題先拆解為規模較小的幾個問題來分別對付, 如果新的問題和原來的問題性質完全相同的話, 就可以用遞迴函式來製作了, 例如: 由一疊考卷中尋找某一位同學的考卷時, 我們可以把一疊考卷均分為兩部份, 先在第一部份中尋找, 再去第二部份中尋找, 這裡每一個尋找的動作都完全相同, 只是資料的多寡不同而已, 也就是上面所說的 "性質完全相同的問題"。
![]()
![]()
這個函式的寫法當然和連加很像, 不過因為 N! 的數字值很大, 我們必須知道 N 值稍微大一點時就不適用了:
![]()
細節請參考函式呼叫時系統堆疊的應用。
因此每一次在呼叫一個函式的時候堆疊上的空間就被佔掉一部份, 一直到函式結束 (回返) 時這些空間才會被釋放出來。 堆疊也是放在記憶體內, 而且通常在程式連結 (link) 的時候就已經指定其大小, 整個程式在執行的時候所使用的堆疊不能夠超過這個大小, 否則就會有執行時的錯誤發生。
例如:在設計一個遞迴程式的時候, 必須要注意到函式自己呼叫自己的次數 (遞迴的次數), 一個有效率的遞迴程式應該很快地將問題切割到可以解決的地步, 而不能顧自地不斷切割問題, 不顧效率, 用空間和時間來換取答案, 如果遞迴呼叫的次數太多, 把堆疊的空間用完了, 反而得不償失, 錯的不知所以然。
Turbo C 中內定的堆疊大小為 4 K bytes, 如果你需要 10 K bytes 的堆疊空間請用 extern unsigned _stklen=10240; 來指定。
我們前面所舉的例子, 不管是連加、階乘、Fibonacci 數列、或是 Selection Sort 都不是運用遞迴很好的範例, 其遞迴的次數和 N 成正比, N 愈大, 遞迴呼叫的次數愈多, 這種情形下通常程式設計者應該採用疊代方式來撰寫程式。
反之前面的 Binary Search 程式, 雖然看起來遞迴程式好像比疊代程式還長, 但是其觀念是比較簡易的, 而且在執行的時候由於每次將問題的大小切為一半, 最多需要 log N (底數為 2) 次遞迴呼叫即可完成, 這種演算法以遞迴函式製作起來就比較划算, 其它類似的演算法還有 Quick Sort, Tree traversal, (老鼠走迷宮) 等等, 請你以後在學到時要特別注意。
![]()
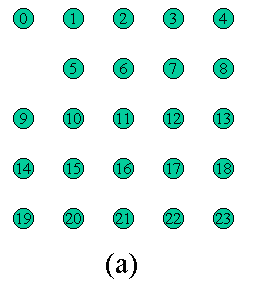
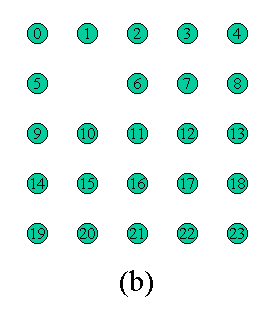
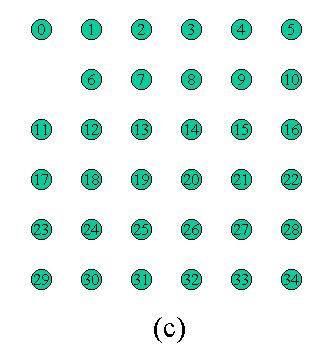
請問由任何一點開始畫, 是否能夠在不重複經過某一點的前題下, 一筆畫過所有的點, 如果有的話, 列印一組可能的解答出來。 上圖中 (a) 可以證明沒有解, (b),(c)則不知道。 讓我們寫一個程式來驗證圖 (a) 是無解的, 並在圖 (b) 及 圖 (c) 中找出各有多少組解答。 如下圖:
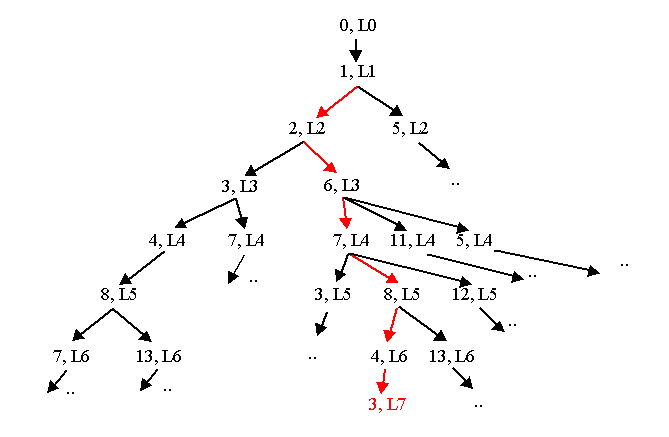
每一個節點代表目前已經畫到該點, 則接下來最多有四種可能性 (上右下左, 其實除了第一點之外最多應該只有三種可能性), 我們可以畫出一樹狀圖來代表所有可能的畫法, 任何一種由最上面節點走到最下層 (第 24 層,L23) 的走法就是一個解答。 觀察這個樹狀圖, 我們可以大約估計最多會有 3^23 種路徑, 當然很多路徑會胎死腹中, 根本走不了幾層就發現沒路可走了, 例如上圖中紅色的路徑, 所以實際上沒有那麼多路徑需要嘗試。
![]()
![]()
| 1000 | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 |
|---|---|---|---|---|---|---|
| 1000 | 0 | 1 | 10 | 9 | 8 | 1000 |
| 1000 | 1000 | 2 | 5 | 6 | 7 | 1000 |
| 1000 | -1 | 3 | 4 | -1 | -1 | 1000 |
| 1000 | -1 | -1 | -1 | -1 | -1 | 1000 |
| 1000 | -1 | -1 | -1 | -1 | -1 | 1000 |
| 1000 | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 |
例如在上圖中, 1000 代表不能夠走過去的地方, -1 代表還沒走過的, 0、1、2、… 則代表走過的順序, 對於任一格而言, 嘗試鄰格的順序可以把它固定為左,上,右,下, 若是該格不為 -1, 則嘗試失敗, 若是四種可能性都失敗的話, 就表示這是一條死路, 當某一格確定為死路時程式需將此格設為 -1, 退回上一格再嘗試下一種可能的路徑, 若在某一次嘗試時成功的話, 則根據本身之序號將該格設為序號加 1 之數值, 接下去一一嘗試該格之所有鄰格。 此時大家應該可以發現所謂的 "一一嘗試所有鄰格" 其實就是遞迴函式的主體, 如下:
請你完成此程式:
注意:
習題: Hanoi Tower
![]()
