二進位的小數表示法

小數
二進位的小數和十進位的小數在觀念上完全一樣,
必須有一個小數點,
小數點的左邊是整數,
小數點的右邊是小數,
每一位數有它的權重,
例如下圖:
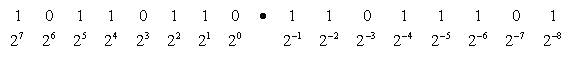
在電腦裡表達小數的方式有兩種,
一種是定點表示法,
一種是浮點表示法。

定點小數表示法:(fixed point)
在電腦裡資料以位元來存放,
而小數點並不需要真的存放在位元內,
我們只要知道哪兩個位元之間是小數點就好了,
或是說我們只要知道每一個位元的權重,
例如上圖即可。
-
一般來講使用定點表示法來表達小數時我們在整個系統中
會將小數點都固定在一個地方,
而不會調來調去,
否則就需要多幾個位元來記錄小數點的位置了。
當然這也是為什麼要叫做定點小數的原因了。
-
在定點小數表示法裡加減法就是二進位的標準加減法,
而乘法必須要把小數點移回來
(你可以用十進位小數乘法去思考)。
-
在高階程式語言內一般都不用定點小數表示法,
因為定點小數表示法所能表示數字的範圍非常有限,
例如上面雙位元組小數點置於第 8 位和第 9 位元之間時,
只能表示 0 到 255 之間每隔 1/256 的那些數字而已,
這樣子範圍的數字在自然界中應用的機會較小,
那為什麼要用這種方式表示小數呢??
簡單地說就是運算速度較快,
定點小數的運算就是標準二進位的運算,
因此很簡單,
硬體製作起來也很便宜,
浮點小數就比較複雜,
軟體模擬比較慢,
硬體也比較貴。
-
自然界中隨便一個數字,
例如十進位 0.1 這個數字當使用二進位定點表示法時,
可能會有誤差,
原因是是十進位 0.1 這個數字用二進位表示時會是
0.000110011001100110011... 的一個循環小數,
以上圖的表示法來說小數以下只能表示八位數,
也就是 0.00011001,
這個數字和原來希望表示的數字會有一點點的誤差,
讓我們把這個數字換回十進位來看看:
也就是 1/256 + 1/32 + 1/16 = 25/256 = 0.09765625,
是蠻接近 0.1 的,
不是嗎,
誤差一定小於 1/256,
而且有一個特性就是實際表達出來的數字的絕對值永遠小於或是等於原來要表達的數字的絕對值。

浮點小數表示法:
所謂二進位的浮點小數表示法
(或是浮點數,
floating point number)
簡單地講和我們十進位中常用的科學記號表示法是類似的,
十進位中我們用十的冪次 (power)
及 0 至 1 之間的小數來表示一個任意的實數,
例如:12345.6789 表示為 0.123456789 * 10^5。
在二進位中我們一樣可以將一個二進位數字 1101110.11011
表示為 0.110111011011 * 27,
這樣子的表示法和定點表示法之間好像沒有什麼不同嘛!!
對!! 這兩個數值的大小當然是完全一樣的,
那為什麼要用浮點表示法呢??
請注意在定點小數表示法之中我們看到它的缺點是絕對值太大的數字會被截斷
(正確的名稱是溢位,overflow)
位數不夠多無法表達大於範圍的數字,
絕對值太小的數 (例如:0.000000001)
也會被截斷 (正確的名稱是無條件捨去,truncation)
只能表達近似的值。
如果是這樣子的話,不知道你有沒有想過...
-
對於一個很大的數字
(例如 123456789012)
定點表示法保証小數點以後一定有固定的幾個位數來表示,
(例如 123456789012.00000011)
可是這樣子的精確度對於大部份的應用來說是沒什麼意義的,
試想太陽到地球的距離多一公里少一公里真的有關係嗎??
光速每秒鐘快一公尺又何妨??
-
對於一個很小的數字
(例如 0.0000000012)
來說定點表示法可能因為小數點後沒有足夠的位數來記錄而將其省略,
上面這個數字就變成 0 了。
如果你說水中含有 0.0000000012 莫耳的氰化鈉,
因為小數點後位數不足而把它當為 0,
這不太好吧!!
這時浮點數表示法就有它的妙用了,
以第一例中一個很大的數字而言:
浮點數由最重要的位數開始只保留一定的位數,
例如 123456789012.00000011 可用 .1234567890 * 1012
來表示就夠了,
這個表達方法所記錄的數字和實際的數字會有誤差,
但是百分比誤差不大。
以第二例而言: 0.0000000012 可用 0.12 * 10-8 來表示,
不需要浪費許多位元記錄 "0",
只需記 12 以及 -8 即可精確地表達這個很小的數字。
舉例來說,
一種簡單的二進位浮點表示法可以一個位元記錄正負號,
七個位元二的補數記錄 2 的冪次,
24 個位元記錄小數,
共 32 位元,
如下圖:

若有一個以此種表示方法的二進位數值:
0 0001110 110000000000000000000000
代表十進位的 0.75 * 214 這個數字。
注意:
和前面的定點小數表示法一樣,
浮點小數表示法在表達任意一個小數的時候,
也常常會有一些誤差,
而且實際所表示的數字的絕對值會小於或是等於原來希望表達的那個數字的絕對值。



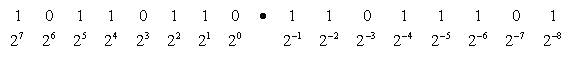
![]()
![]()

