根據 zodiac 的數值來列印十二生肖中文字有三種作法 第一種是運用條件判斷敘述 if-else 來檢查 zodiac 變數的資料， 然後運用 printf() 敘述來列印； 第二種是運用 switch (zodiac) { case 0: printf() break; .... } 來列印； 第三種是運用字元指標陣列 const char *zname[] = {"鼠", "牛", "虎", "兔", "龍", "蛇", "馬", "羊", "猴", "雞", "狗", "豬"}; 配合 printf("%s\n", zname[zodiac]); 來列印， 當 zodiac 變數內容為 0 時列印陣列的第一個元素 zname[0]， 當 zodiac 變數內容為 11 時列印陣列的最後一個元素 zname[11]。 (陣列、常數字元指標型態、字串常數過幾個星期會在課堂中一一解說。)
這個答案是連續正整數平方和級數 12+22+32+...+n2， n 的範圍由 0 到 1023， 可以直接用公式 n(n+1)(2n+1)/6 計算這個級數， 因為 n 的數值不是很大， 也可以直接用迴圈模擬平方和加總來計算。
| 圓的個數 n | 1 | 2 | 3 | 4 | 5 | ... |
| 區域個數 f(n) | 2 | 2+2 | 4+4 | 8+6 | 14+8 | ... |
這一題和 求數列第 n 項 一樣都是數列， 但是那一題題目直接告訴你數列的第 n 項 f(n) = f(n-1) + (n-1)， 首項 f(1) = 1。
做這個例子的時候， 也許會覺得這根本是一個數學的問題， 程式的實作沒有什麼困難度， 事實上資訊相關許多領域裡寫程式的目的就是為了解決各式各樣問題， 這個時候數學其實是一個用到最多的工具， 如果放棄數學直接用暴力法解問題的時候， 雖然對於數字比較小的範例來說是比較容易掌控的， 但是當問題的規模變大的時候， 常常會讓電腦筋疲力竭而找不到答案， 這個狀況特別容易出線在資安的應用中。
特別留意題目敘述裡數字的範圍: m-n < 10000， 但是沒有 n 的範圍， 保險的話應該是假設用 64 位元的整數
隱藏測資的 trick: n 跟 m 可以為負數
想一想上面的作法是不是還可以運作?
有三種狀況：
1. n>0, m<0：輸出 1
2. n<0, m<0, m<n：輸出 1
3. n<0, m≥n：上面二次不等式仍然正確
文文十進位 6 位數的密碼編碼成 7 個英文字，
兩個英文字母的距離就是文文的密碼，例如：
POKEMON 對應的密碼是 146821
'P' 的內碼是 80
'O' 的內碼是 79
'K' 的內碼是 75
'E' 的內碼是 69
'M' 的內碼是 77
'O' 的內碼是 79
'N' 的內碼是 78
所以密碼是 80-79=1, 79-75=4, 75-69=6, 77-69=8, 79-77=2, 79-78=1
由鍵盤讀取資料的時候有兩種方法： 第一種是用 scanf() 的 %s 讀入字串 (字元陣列)， 另一種是用 getchar() 一個字元一個字元讀。
for (i=1; i<=n-7; i+=7)
for (j=0; j<6; j++)
printf("%d ", i+j);
n -= n%7==0;
for (j=i; j<=n; j++)
printf("%d%c", j, j==n?'\n':' ');
這一段程式就只剩下一次除以 7 計算餘數的動作了。
另外外層迴圈只執行到 n-7，
最後幾個再用第二個迴圈來列印，
換列字元前面就不會多出一個空格字元，
但是要注意如果 n 是 7 的倍數時只要印到 n-1 即可。
另外一種想法是在判斷完最高票候選人之後， 把那個候選人的票數和 A 候選人的票數交換， 這樣子 B 和 C 就是第二高票和第三高票， 就可以直接加總這兩個變數來判斷， 在最後輸出當選者的時候， 會發現需要在上面判斷的過程中還是需要判斷誰是第二高票， 也需要把最高票候選人和次高票候選人紀錄在變數裡面， 最後才能輸出當選者。
更一般化的作法就是把票數和後選人代號(A,B,C 的 ASCII 碼)先放進一個二維陣列中， 然後依據票數排序 (可以用 qsort)， 判斷第二高票和第三高票的票數和是否大於第一高票的票數， 然後輸出第一高票或是第二高票候選人。
如果是不能跟別人借空瓶的話， 實作時可以用迴圈來模擬整個過程， 迴圈中每次喝 3 瓶， 以 3 個空瓶換回一瓶， 過程中以變數紀錄目前有多少瓶， 總共喝了多少瓶， 一直執行到不夠 3 瓶為止， 把最後 1 或 2 瓶喝掉， 程式結束。
不過再仔細分析一下， 如果 n = 2k + 1, k>0， 則可以喝到 3k+1 瓶， 等於說 2 瓶 2 瓶一組總共有 k 組， 多出來這 1 瓶可以借給任何一組變成 3 瓶， 喝掉、3 個空瓶換回 1 瓶再還回去， 這個過程可以喝掉 3k 瓶， 最後一瓶再直接喝掉。 另外如果 n = 2k + 2, k>0， 則可以喝到 3k+2 瓶， 推理方法同上。
能夠仔細分析而得到這樣子的數學式子的話， 計算的速度遠比模擬要快得多， 模擬就好像不動腦的暴力作法， 雖然電腦的速度比人快很多， 但是我們很快地就發現日常中有太多工作如果暴力進行的話， 很快就把電腦速度的優勢耗盡， 所以請建立正確的觀念， 能夠避免暴力法浪費算力的時候一定要避免。
如果可以跟別人借空瓶的話， 最後需要把所有借來的空瓶還給別人， 不能負債， 實作時當然還是可以用迴圈來模擬整個過程， 迴圈中每次喝 3 瓶， 以 3 個空瓶換回一瓶， 過程中以變數紀錄目前有多少瓶， 總共喝了多少瓶， 一直執行到不夠 3 瓶為止， 如果剩下 1 瓶的話就直接喝掉， 如果剩下 2 瓶的話， 喝掉並且跟別人借一個空瓶， 以 3 個空瓶換回一瓶， 喝掉， 把空瓶還給別人， 程式結束。
不過再仔細分析一下， 如果 n = 2k, k>0， 則可以喝到 3k 瓶， 等於說 2 瓶 2 瓶一組總共有 k 組， 可以跟別人借 k 個空瓶使得每一組變成 3 瓶， 每一組喝掉 2 瓶、 以 3 個空瓶換回 1 瓶， 再喝掉、得到 k 個空瓶再還給別人， 這個過程可以喝掉 3k 瓶， 沒有欠別人任何空瓶。 另外如果 n = 2k + 1, k>0， 則可以喝到 3k+1 瓶， 多的那 1 瓶直接喝掉， 不能跟別人借空瓶， 因為借 2 瓶的話最後空瓶會不夠還。
請參考投影片說明，
+ ++ +++如果還是有問題， 可以更進一步簡化成每一列都相同的矩形:
+++ +++ +++如果基本的「靠左對齊的三角形」沒有問題， 就可以進一步構思每一列都需要填滿的靠左對齊三角形， 也就是要求每一列印出的字元數都相等:
+__ ++_ +++接下來可以回到題目要求的「靠右對齊的三角形」:
__+ _++ +++完成要求以後還可以進一步思考如何完成「等腰三角形(金字塔)」:
__+ _+++ +++++注意要完成這個要求的話，每一列需要有奇數個 '+'， 最後可以再回到我們放在實習裡的「金字塔列印」， 橫向地列印多個高度不等的三角形， 例如下面是高度 4/3/2/1 的四個三角形:
___+ __+++____+ _+++++__+++__+ ++++++++++++++++上圖中以底線字元 '_' 來代替空格字元 ' '， 比較容易看出來， 請參考投影片。
要提昇自己的分析能力就需要多做延伸性思考, 多練習抽象化、簡化題目的能力。 咦?! 這個題目為什麼叫做「數字」三角形??
因為每天購買的的饅頭數沒有特別的規則， 所以沒有辦法看成特殊有規律的數列用數學方式來計算， 只能根據一天一天購買的饅頭的數量和當天的價格來計算， 需要使用迴圈的語法來實作。
基本上需要以迴圈把每一項 x 列印出來， 因為給了一個末項的整數， 可以作為迴圈結束的檢測， 由首項開始列印， 當到達末項 e 的時候， 迴圈就可以結束， 也就是比對 x!=e 的時候就列印。
如果這個數列每一項 x 都是浮點數， 檢查是否到達末項就需要用不等式來檢查， 這個時候公差的正負號就有差別， 公差大於 0 時， for 迴圈的寫法如：for (x=s; x<=e; x+=d)， 公差小於 0 時， for 迴圈的寫法如：for (x=s; x>=e; x+=d)。
N B[0] B[1] B[2] ... B[N-1]輸出為 B 序列的差分序列 A[0] A[1] A[2] ... A[N-1]
雖然題目的描述一點複雜， 多介紹了 B 序列是差分序列 A 的「前綴和」概念， 不過耐心分析題目的描述之後， 應該可以歸納出來計算差分序列的法則為： A[0]=B[0], A[i]=B[i]-B[i-1], i=1,2,...,N-1， 可以練習一下 for 迴圈。
2 6 1 5 6 8 9 13 3 4 5 7 8 11 4 6 7 14 16 23 6 9 12 13 16 23輸出測資：
2 3這組測資有兩個測試案例， 每一個測試案例有兩列資料， 每一列有 6 個由小到大排列的整數， 題目要求比對這兩列資料裡有幾個共同的數字， 例如第一個案例中有 2 個共同的數字， 分別為 5 及 8； 第二個案例中有 3 個共同的數字， 分別為 6, 16, 及 23。
因為輸入的兩個序列已經排好順序， 可以很直接地運用平常合併兩個有序序列的方法來比對， 就是兩個序列分別維持一個由 0 開始的指標， 用一個單一的迴圈， 迴圈中每一次比較兩個序列中指標指到的元素， 如果相同的話就把指標同時往後移動， 同時紀錄出現一組同的數， 如果不等的話， 先往後移動指向比較小的那個指標。 類似應用請參考投影片說明，
別管 d136 是什麼題目了， ZeroJudge 上已經找不到了， 據說通過比例曾經是 1/130， 哈哈，通過的就是原來出題的人， 可能不是題目太難而是有一些錯誤。
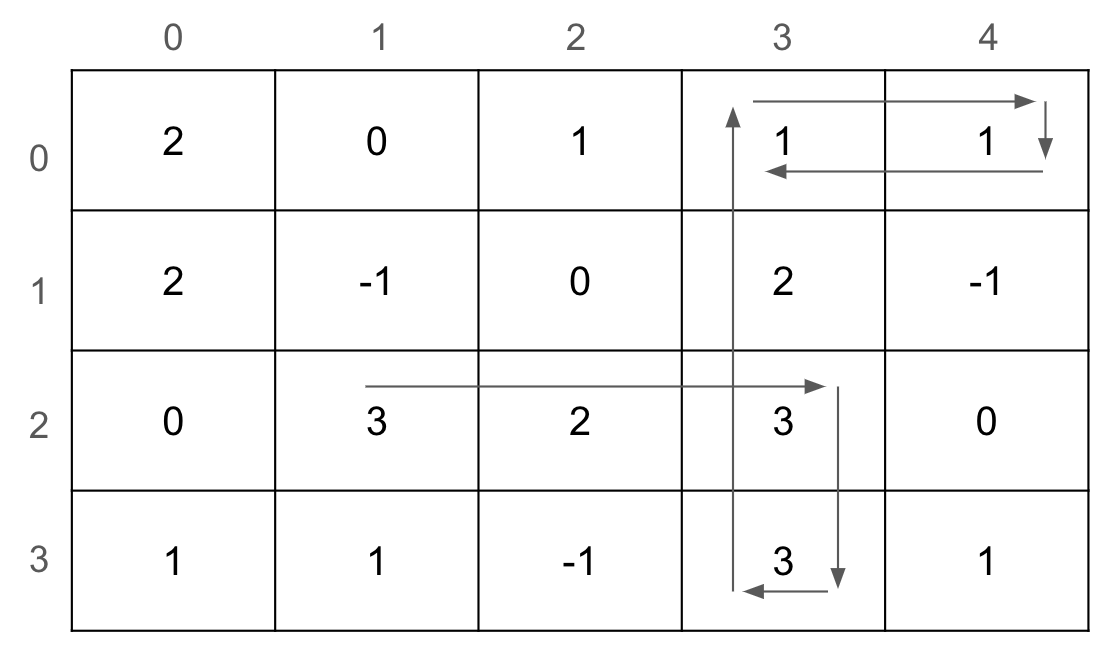
徹底研究題目的規則以後， 還好沒有退回前幾步的動作， 所以不需要使用 DFS/遞迴函式 來解， 只是一個迴圈控制的問題而已， 基本上還是用模擬的方法來找出答案。
| Step | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| (row,col) | - | (2,1) | (2,2) | (2,3) | (3,3) | (2,3) | (1,3) | (0,3) | (0,4) | (0,3) |
| score | 0 | +3=3 | +2=5 | +3=8 | +3=11 | +2=13 | +2=15 | +1=16 | +1=17 | +0 |
| action | - | → | → | →, ↓ | ↓, ←, ↑ | ↑ | ↑ | ↑, → | →, ↓, ← | stop |
因為寶石撿走以後每一格的寶石數會減 1， 上面這張圖配合列表其實要表達整個狀況還缺一點點， 參考 投影片 裡的動作細節應該更清楚一些。
看了半天都沒有程式， 這是在講程式怎麼寫嗎???
其實把程式碼貼在這裡， 對於想要快速完成程式、 繳交作業、 刷題當然有極大的幫助， 但是對於想要培養、提昇自己設計能力的同學幫助就不太大了， 常常會落得別人設計得很高興， 自己卻是知其然而不知所以然 (很多高中生的確是這樣)， 只是在練習打字殺時間而已， 平常在設計階段會遇見的問題、用力解決的問題， 常常在別人已經寫好的程式片段裡面是看不到的。。。
要提昇自己的程式設計能力， 其實是要在自己心裡頭建立出程式運作過程的圖像， 也就是要能夠具象化程式對於上面的範例所作的細部動作， 掌握以後再換成程式就容易了， 過程中你也才會看到設計一個解決方法應該要看到的問題。
好了，到底程式在哪裡呢?? 上面所有需要的變數設計出來， 每一步座標的修改， score 的修改， 移動的方向的修改 (需要一個小迴圈在不斷遇見邊界或是牆壁時連續地修改方向)， 各個動作都換成程式以後， 放進一個大迴圈裡， 結束條件設為「當到達那個座標時， 座標的寶石數為 0」的時候， 一切就幾乎完成了。
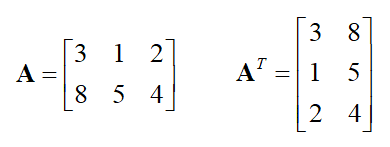
6 3 0 5 0 4 2 0 0 0 1 0 1 0範例輸出:
2第一列有兩個整數 N 及 T， 代表兩個陣列都有 N 個元素， T 是起始的位置， 0≤T≤N-1， 針對這一組範例測資， 用模擬的方法來了解題目的特性， 第一個陣列 x[] 指出下一個位置， 因為每一個位置只能經過一次， 所以在模擬過程中， 陣列 x[] 的任何一個元素儲存的資料最多只會使用一次， 可以利用這個陣列來紀錄哪些位置已經走過了， 走過第 i 個位置就把 x[i] 設為 -1 (下圖中用 * 表示)， 如此第二次走到這個位置的時候模擬就結束了。 下面我們以 x[] 陣列的內容變化來顯示模擬的過程， 同時也需要紀錄過程中吃到了幾個布朗尼。
位置 布朗尼個數 0 1 2 3 4 5 0 5 0 4 2 0 0 0 5 0 * 2 0 1 0 5 0 * * 0 2 0 5 * * * 0 2 * 5 * * * 0 2
這個問題可以說是 c296. 定時 K 彈 的簡化版，c296 如果直接模擬的話是會超時的， 主要是因為 c296 所經過的位置需要刪除， 同時下一位置是用相對的步伐數來指定的， 所以那個問題可以說是一個每個元素資料不斷改變的 range sum 問題， 可以運用 segment tree 或是 binary indexed tree 來得到符合時間限制的解， c296 其實是一個很經典問題的實例 - 約瑟夫問題(Josephus Problem)。
更一般化的 range sum query 問題還包括 range maximum query (RMQ) 或是 range minimum query (RmQ) 問題， 分別是求區間中的最大值或是最小值， 同時陣列中所有的元素隨時會有修改， 所以就沒辦法像前面簡化的 RSQ 問題用「前綴和」來解， 尤其當 n 與 m 的數值很大時， 有非常多的重複計算， 一定會得到超時 (TLE) 的結果， 一般有效率的作法是「線段樹 (Segment Tree)」, 影片, 或是「芬威樹(Fenwick Tree), (樹狀樹組, Binary Indexed Tree)」影片。
很快計算一下， 如果飽足度都是 100 且 n 為 500 且查詢區間是全部的話， 飽足度總和是 100*500*500=2.5*107 還小於 231， 所以可以用 int 型態來處理。 因為所有的飽足度在查詢過程中都是定值， 所以是有限制的 RSQ 問題， 可以用二維的前綴和來加速查詢。
每一個點 (i,j), 1≤i,j≤n 的二維前綴和 B[i][j] 定義為左上角 (1,1) 且右下角 (i,j) 的矩形內所有食物的飽足度之和。 查詢左上角為 (x1,y1) 且右下角為 (x2,y2) 的矩形區間內食物的總飽足度， 就可以根據二維前綴和矩陣 B[][] 來計算， 也就是 B[x2][y2] - B[x2][y1-1] - B[x1-1][y2] + B[x1-1][y1-1]。
實作的時候二維的前綴和陣列可以定義為 int B[501][501]， 多出來的一列 B[0][j] 和一行 B[i][0] 都設為 0， 上面查詢式子當 x1 或是 y1 為 1 時才不會讀取沒有定義的前綴和。
如何計算二維前綴和矩陣 B[][]：
1. 每一列先計算一維前綴和於 B[i] 陣列中， i=1,2, ...,n，
也就是 B[i][j] = A[i][1]+A[i][2]+...+A[i][j]
2. B[i][j] = B[i][j] + B[i-1][j], i=2,3, ...,n, j=1,2,...,n
當然如果食物的飽足度在查詢過程中一直有改變， 就需要藉由二維的線段樹或是二維的樹狀數組來滿足一般化的 RSQ, RMQ, 或是 RmQ 查詢。
13 = 6 * 2 + 1 6 = 3 * 2 + 0 3 = 1 * 2 + 1 1 = 0 * 2 + 1 13 ⇒ 1101上面的動作基本上就是整數除法和整數除法的餘數，
如果透過陣列由最低位開始來轉換 x 的進位制的話：
如果想從最高位開始轉換 x 的進位制的話，
需要找到總共有 w 位數：
基本的方法就是模擬，
但是又不需要完全依照題目的說明來模擬，
把所有資料讀到整數陣列裡，
每一個元素可以是 char, short, 或是 int，
因為輸入數列中元素個數不多，
可以挑選機器最容易處理的 int 型態。
每一個步驟不需要真的把資料刪除、
也不需要把數列反轉過來，
只要指定開始印的元素，
需要列印的元素個數一次比一次少，
運用迴圈列印，
就可以達成題目的要求了。
以上面第一個範例測資來說，
首先把 99 77 66 44 11 讀到陣列裡，
這個標示的動作也可以等到偵測器處理完了以後再一起處理，
以每一個炸彈為中心檢查四周是否有有效的偵測器 (==5)，
如果有就加總在會被偵測到的炸彈數中，
如果沒有就加總在未被偵測的炸彈數中。
期中考
一種作法是以兩層的迴圈反過來由最後一列往前、
每一列由最後一行往前，
和 n-i 列 n-j 行的元素比較，
如果有任何一個不等就失敗了。
仔細思考一下，
其實資料不需要放在二維陣列中，
所有的資料直接放在一維陣列中，
然後只要是一個一般的迴文 (Palindrome) 就符合「轉 180 度完全一樣」了。
範例輸入一:
範例輸入二:
注意這個計數系統使用的符號 1 就是代表 1 個，
符號 2 就是代表 2 個，
...
符號 9 就是代表 9 個，
數字 11 代表 10 個，
...
數字 19 代表 18 個，
數字 21 代表 19 個，
題目保證轉換出來的數字不會超過 2147483647，
所以可以用 int 型態，
但是輸入應該用字元陣列，
另外這個計數系統沒有辦法表示 0 個。
還有另外一種 9 進位制的想法，
就是讓 9 個符號 {1,2,3,4,5,6,7,8,9} 分別代表數值 0,1,2,3,4,5,6,7,8，
雖然看到一個數字 9124 比較容易混淆，
它等效的十進位數值是 8*93+0*92+1*91+3*90=5844，
就好像讓 9 個符號 {a,b,c,d,e,f,g,h,i} 分別代表數值 0,1,2,3,4,5,6,7,8，
看到一個數字 iabd 時，
等效的十進位數值就是 8*93+0*92+1*91+3*90=5844，
這個數字系統就可以表示 0 這個概念，
例如 a3a2a1a0
所表達的數值用十進位來看是
(a3-1) 93 + (a2-1) 92 +
(a1-1) 91 + (a0-1) 90，
這樣子也是一個完整的計數系統，
只是和題目裡描述的「9 的下一個數字是 11，
19 的下一個數字是 21，99 的下一個數字是 111」，
還有測試範例一： 19 ⇒ 18，測試範例二：111 ⇒ 91 不符合而已。
範例輸入:
程式只需要一個簡單的迴圈，
迴圈裡面讀入一個字元 c，
再讀入一個十進位數字 n，
然後以迴圈輸出重複 n 次的字元 c 即可。
題目後面提示的動畫其實是很重要的，
只是 1. 這個動畫並不是說明題目裡的範例測資二，2. 圖片裡面有給測資，但是有錯誤 0 0 3 2 應該改成 0 0 2 3，
3. gif 動畫太快了，你需要會速讀才能夠看出來它的動作，
修改過的動畫如下
或是參考 投影片 裡面的分解動作，
麻煩你一步一步看。
或是參考下圖
ZeroJudge 上其實很多的執行時間都是花在輸出和輸入上，
以這個題目來說，
要不斷地用 printf() 把一個一個排列印出來是很花時間的，
如果準備一個陣列，
把所有要輸出的排列都先寫在陣列裡，
最後一次輸出，
會讓時間降低 50 倍。
題目要求找到序列的中位數，
最直接的方法就是排序，
所以請把整個序列用一個迴圈做出來放在陣列裡面，
然後用 qsort() 還序，
再輸出第 (n+1)/2 項 (序列由第 1 項開始)。
炸彈引爆之後將 Xi 設為 0，
最後輸出 N 個炸彈的最終狀態。
範例輸入#1:
也可以練習一下寫一個二分法來找出序列 F(1), ..., F(31)
中第一個大於等於 A 的元素，
也就是我們講二分搜尋法時的 lower_bound() 這個函式，
給你 m 支文字都不同的籤，1≤m≤50000，
籤文長度最短是 1、最長是 100，
請問可以抽出幾種聖筊組合。
最直接的想法是用兩層的迴圈把所有 m(m-1)/2
種組合都串接看看，
總長度是奇數的一定不是，
其它組合再用一層的迴圈測試看看是不是包含兩個完全重複的字串。
這樣子的運算量會在 50000*50000/2*100/2 ~ 6.25*1012，
因為機器差不多每秒執行 109 個指令，
看起來會是 TLE，
需要找到比較有效率的作法。
題目裡有一個很有意思的提示，
就是「兩隻籤如果是聖筊，
簽文接在一起誰先誰後都沒有關係，
一定會是兩個重複的字串」。
好像只是有點神奇而已，
和怎麼加速這個問題的解法有關聯嗎???
再用剛才的例子來想一下，
兩支籤文分別是 A = piep 和 B = ie，
第一個籤文 A 比較長，
所以重複的子字串 C = pie 會在 A 裡面就開始重複了，
像是 piep，
第二個籤文 B 比較短，
會出現在第一個籤文的中間，
重複子字串 C 的後半段，
也就是第一個籤文 A 可以看成 C || D，
本例中 D = p，
也就是說兩個字串的串接 A || B 會等於 C || C，
也會等於 DBD || B = DBDB，
看到這裡當然另外一種串接方法 B || A = C' || C' = B || DBD = BDBD，
也會得到重複的兩個子字串 C' = BD = iep。
重點在於這 m 個字串如果要成為上面的 A 字串的話，
字串裡面需要看到 DBD 的樣子，
也就是 A 字串裡面的前綴 D 會在 A 字串尾巴重複出現，
剩下中間的部份 B 又出現在 m 個字串中，
我們就找到了一組聖筊 (A, B)。
因為要確定 B 是否有出現在 m 個字串當中，
m 個字串需要先用 qsort() 排序，
然後再做二分搜尋 bsearch()，
前綴字串 D 的長度最短是 1，
最長是 (|A|-1)/2，
可以用一個迴圈去列舉，
驗證是否出現在 A 字串尾巴。
則需要第二層迴圈來比對，
如此最大的運算量大約是 50000 log50000 + (100-1)/2 * (100-1)/2 * log50000 ~ 820。
題目要求計算下面定義的數列 g(n) 的十進位位數:
首先任何一個十進位整數字 x 的位數是 1+floor(log10x)，所以
只要算出 log n! / log f(n) / log g(n) 就能算出 n! / f(n) / g(n) 的位數。
令 E(n) = log n!, F(n) = log f(n), G(n) = log g(n)，
可以寫出遞推的關係式如下：
E(n) = E(n-1) + log n, E(1) = log 1 = 0
可以畫一張圖來顯示計算的先後順序：
一種是用整數陣列，
把需要排順序的元素的註標存放在中介陣列 index[] 裡，
然後在比對大小的 compare() 函式中間接地存取 data[] 陣列內的資料，
例如：
另外一種是用指標陣列，
這個方法比較好，
data[] 陣列不需要是全域的陣列，
我們把需要排順序的 data[] 陣列元素的指標存放在指標陣列 ptr[] 裡，
在比對大小的 compare() 函式中透過指標來存取 data[] 陣列內的資料，
例如：
基本上以換列字元為分割點所造成的問題，
是因為換列字元本身是 white space 的一種，
stdio.h 的工具函式在執行很多轉換命令時都會自動跳過所有的 white space，
所以能夠使用的工具會少一些，
可以使用 getchar(), fgets()，
將一列資料讀到字元陣列以後，
再使用 sscanf() 或是 strtok() 工具函式去讀出一個一個整數，
當然也是可以用
以第一列的測資為例，
題目希望你讀入一個數字 3 以及字串 ABCEHSHSH，
然後 3 個字元為一組來反轉，也就是
主要是練習兩層迴圈的控制以及字串的反轉，
外層迴圈可以用目前處理群組的起始點作為控制變數，
每次增加群組的字元數，
內層迴圈是反轉字串的，
可以用兩個控制變數，
一個紀錄群組起點字元所在位置，
另一個紀錄群組終點字元所在位置，
迴圈內容是利用一個變數交換這兩個字元，
迴圈控制變數修正的地方把起始點加 1，
把終點減 1，
只要起始點小於終點迴圈繼續執行。
範例輸入#1:
範例輸入#2:
四種規則分別實作如下：
範例輸入一:
範例輸入二:
請特別注意數字範圍很大，
需要使用 long long 型態的整數。
有些遞迴的題目真的很經典，
非常值得仔細思考，
例如
POJ 2651: So you want to be a 2n-aire?
就是電影「平民百萬富翁」情節，
請參考 投影片
不論你是不是已經清楚題目的要求，
下面簡要的描述應該是對的：
注意因為會有多種方式得到指定的分數，
請找出所有可能的方式，
輸出分數的計算方法時，
不要管數字的順序，
只需要把「加號」、「乘號」拿出來排序，
「加號」的順序在「乘號」之前，
例如輸出的順序：
撰寫這個程式的時候，
可以由我們上課談的遞迴 DFS 的數數字程式架構開始，
遞迴函式裡面最主要就是決定：
什麼是結束條件 (滿足時紀錄或是輸出結果，return 不要再遞迴下去)，
這題就是計算出來的分數和指定的相同，
然後列舉每一個決策點所有的可能性，
這題中就是「加號」和「乘號」，
先試哪一個呢?
因為題目要求列印方法的時候「加號」優先，
所以應該先試「加號」，
這樣子在找到滿足結束條件時，
直接輸出計算的方法就可以。
DFS 遞迴函式執行過程中會決定是走加號分支還是乘號分支，
走加號分支時計算方法是 "+ 目前計數器分數"，
乘號分支時的計算方法是 "* 2"，
直接把這個計算方法紀錄在字元陣列裡就可以，
這個陣列可以定義在 main() 裡面，
然後傳進遞迴函式裡，
當然競賽程式那裡會告訴你定義成全域變數，
自己曉得考量點在哪裡就好，
不論是哪一種，
在決定哪一個分支的時候，
把計算方法附加在先前的計算方法之後，
所以有一個很重要的狀態變數就是目前計算方式的長度，
有這個資料，
才有辦法附加在最後，
這個資料應該要設計成遞迴函式的參數。
在上面這個遞迴函式內容設計的同時，
有另外一件事情是同時、甚至優先思考設計的，
就是遞迴函式的參數，
DFS 遞迴函式的參數需要紀錄搜尋的狀態，
以這個題目來說，
需要包含獲得的分數、
鈴鐺分數計數器的數值、
還有到目前為止計算方式的長度，
注意在退回到前一個決策點時，
需要立即回復到先前的狀態，
這三個參數在一個遞迴函式結束 return 到前一層的時候，
立即就切回前一層的三個變數，
所以資料立刻能夠回覆到前一個決策點。
所以需要在每一步驟決定需要使用 Ctrl+C 還是 Ctrl+V，
可以想像這是一個決策樹，
每一個決策點的狀態是 (目前的 * 字元數, 目前剪貼簿中的 * 字元數)，
這個決策樹隨步驟數增加而擴張得非常快，
這個問題就是希望找到最短的決策路徑能夠得到指定數量的 * 字元數，
因為整個樹長大得很快，
如果做深度優先的搜尋有可能需要極多的時間，
廣度優先的搜尋比較適合用來找最短的決策路徑，
但是需要額外的 佇列(Queue) 資料結構。
如果講到這裡還是覺得沒有概念，
需要從簡單的範例著手推演一次，
才能夠比較快精確地掌握。
請參考 投影片 裡面的分解動作，
麻煩你一步一步看。
手動畫出這個問題的決策樹之後，
會發現這個樹有一些特性其實可以運用：
第一、如果不要求動作數量最少的話，
這個問題有很簡單的解，
就是 Ctrl+C, Ctrl+V, Ctrl+V, ...., Ctrl+V,
例如要求做出 50 個 * 字元，
就是 1 次 Ctrl+C，
加上 49 次 Ctrl+V，
所以任何決策路徑如果長度超過指定的 * 字元個數的都不是答案；
第二、任何動作都不會減少 * 字元的數量，
所以一旦某一個決策路徑上 * 字元數量超過指定的數量時，
這個決策路徑一定是錯的；
第三、Ctrl+C 後面一定是 ctrl+V，
可以把這兩個動作綁在一起，
路徑長度一下子會增加 2；
第四、所以可以看到這個決策樹兩邊不太平衡，
Ctrl+V 那一邊增長的速度比較慢，
Ctrl+C, Ctrl+V 那一邊增長得比較快，
應該要先看 Ctrl+V 這一邊，
連同第一點應該可以比較快找到比較短的可行決策路徑，
如此可以得到比較嚴格的限制，
在搜尋的過程中一旦超過這個限制的決策路徑都不是我們要的。
有了上面講的這些特性，
有可能 DFS 也不會花太多時間，
因為路徑的長度都有上限。
設計解決這個問題的 DFS 遞迴函式的步驟和前面
d621 兔子跳鈴鐺 是一樣的，
需要去設計遞迴函式裡面的內容，
包括結束條件 (前面我們談了好多個條件)、
和每一個決策點所有的可能性 (Ctrl+C 和 Ctrl+V)。
然後需要設計遞迴函式的參數來紀錄搜尋的狀態。
這個題目要求把所有最短決策路徑上的決策印出來，
如果有多個決策路徑的長度相同的話，
要依照 'V' > 'C' 的字典順序把決策動作一一印出，
題目的這個要求會造成程式需要比較多的記憶體，
把搜尋過程中所有路徑長度與目前最短路徑的長度相同的路徑都紀錄起來，
有點難估計最短路徑會有多少條，
所以這時只能拿題目給的「路徑數不大於 6000」，
還有「路徑長度不大於 10000」來準備記憶體，
例如 char minpath[6000][10000]; 這個陣列需要 60MB 的記憶體，
不過二元的決策 Ctrl+C 和 Ctrl+V 其實只需要 1 個位元就可以紀錄，
也就是一個位元組最多可以紀錄 8 個動作，
例如以位元 0 代表 Ctrl+C，
以位元 1 代表 Ctrl+V，
這個其實沒有很難設計，
首先定義兩個陣列：
這一題是「e550. 00722 - Lakes (CPE 2013/03/25 #5)」的延伸，
「d626. 小畫家真好用」也是幾乎一樣的題目。
先簡化這個問題一點點，
如果只計算 f(f(f(x)))，
可以先計算 y = f(f(x)) 然後再計算最後一層 f(y)，
最後的答案可以用部份的答案 y 再進一步算出來。
回憶一下，
一個計算複合函數 f(f(f(x))) 的遞迴函式可以寫成這樣：
如果函數複合的次數和輸入 x 不是預先知道的，
而是從串流中讀到幾個 f 就是要複合幾次，
輸入 x 是在輸入串流中的一個十進位數字，
例如：
f f f 7
就是計算 f(f(f(7)))，
程式可以寫成
注意：剛才是從撰寫遞迴函式的角度來看，
輸入串流裡的資料是在遞迴的過程中指定複合函式的種類和次數，
但是如果從運用遞迴函式規範輸入格式的角度來看，
程式運作時呼叫遞迴函式，
限制了輸入一定要能夠用 prefix (preorder) 的方式來描述一個運算，
這個運算必須要能夠做出一個數值，
這個在計算理論裡面我們說是一個 pushdown automata，
在描述程式語言的語法時我們說是 LL1 的語法，
程式只要能夠符合 LL1 語法，
就可以用遞迴函式來檢查語法並且建立 parse tree。
程式可以有一點點的變化是在結束條件的設定上，
如果是在資料個數為 2 時就直接做最大或是最小的比對而不要遞迴下去，
雖然遞迴函式比較長一些，
而且覺得函式裡有功能重複的程式碼，
但是因為最下層有 n 個節點時，
倒數第二層有 n/2 個節點，
也就是避開了一半的遞迴函式呼叫，
上傳 ZeroJudge 時可以發現執行時間由 5ms 縮減為 2ms，
可以看到在遞迴函式內所做的事情很少的時候，
遞迴函式的呼叫所佔的時間就很大，
需要避免，
這種情況在很多遞迴的程式裡都會遇到，
很簡短的程式有的時候就是要花兩倍的時間才能算完。
運用遞迴的 DFS 來解這個問題的時候，
需要把上面這個遊戲的過程想成如下圖的決策樹：
1. DFS 遞迴函式的結束條件就是在限制的那一列或是行上面，
所有的分數已經都被挑完了，
為了完成上面兩個部份的功能，
當玩家挑選一個數字以後，
需要把它標示起來，
才知道被挑過，
如果整個盤面的分數紀錄在一個全域的二維整數陣列裡，
因為分數是正的，
所以呼叫一個遞迴函式挑選某一格的數字前，
可以把那一格的分數乘上 -1，
如此遞迴下去可以根據正負來分辨是否被挑過，
一個遞迴函式結束時，
代表退回前一層來挑選下一個選項，
在這個動作之前，
需要再把分數乘上 -1 來還原成沒有被挑選的狀態。
精簡一點的參數也可以把兩人的分數合併起來成為一個整數，
一個人的得分是正的，
另一個人的得分是負的，
遊戲結束的時候如果分數是正的代表第一個人贏了，
分數是負的代表第二個人贏了，
分數是 0 代表平手。
另外遞迴的深度和限制的列號/行號其實也可以合併成一個整數參數，
例如正的就代表奇數層，
絕對值就是限制的列號，
負的就代表偶數層，
絕對值就是限制的行號。
寫完這一題以後，
可以想一想能不能寫一個和人玩的遊戲，
電腦速度很快，
在人做出一個決定以後，
可以針對下一層的幾種決定去評量哪一個是最有利的，
也就是固定下一層的決定，
然後接續下去把所有的可能性都試過一遍，
看看哪一種決定對於電腦最有利?
上面這個方法，
可以藉由將所有活動的結束時間排序以後，
依序檢查每一個活動的起始時間是不是會議室的活動已經結束，
就可以很快判斷究竟可以容納幾個活動。
上面的描述顛倒過來思考也是可以的，
就是以每一個活動的起始時間來排序，
從最後一個開始的活動指定會議室，
逐漸根據活動的起始時間往前看，
如果那個活動的結束時間太晚，
會議室已經排給其它活動，
這個活動就排除掉，
如此逐步根據活動起始時間由後往前來安排會議室，
也會得到一模一樣的最佳結果。
可以把起始時間和結束時間放在 int time[20][2]; 的陣列裡，
運用 qsort() 根據起始時間或是結束時間來排序。
我們平常真正使用的參數，
會希望它的週期越大越好，
最好就是 M，
這個題目希望能夠找出某一組參數所生成序列的週期。
觀察上面這個生成的公式，
可以看到一旦重複產生某一個數字，
後續生成的序列就開始重複了，
所以要找出序列的週期，
就是要看序列什麼時候出現一模一樣的數字。
因為題目限制了 Z,I,M <= 9999，
同時序列的元素 0 <= L < M，
所以可以用一個 10000 個元素的陣列來紀錄哪一個元素出現過，
每生成一個數字就需要去檢查一下這個陣列，
如果這個數字已經出現過，
代表序列開始重複。
週期是第一次出現以後到第二次出現時序列共有多少數字，
所以這個陣列不只需要紀錄某一個數字是否出現過，
還需要紀錄出現的流水號，
如此在第二次出現時，
可以拿當時的流水號減掉陣列裡紀錄的流水號來得到序列的週期。
首先在題目要求的這個範圍 [1,1000000] 內，
數列是確定都會收斂到 1 的，
而且最大的週期是 525 (n=837799)，
暫且不用理會超過這個範圍的 n 起始的數列會不會收斂，
Collatz conjecture 是認為會收斂的啦！
題目雖然沒有限制測資中會給多少次的查詢，
但是從剛才給的數據，
對於直接模擬的程式來說，
可能 10~20 次查詢就超過 1 秒了。
這些查詢的範圍可能有相當的重複，
所以第一件事情需要避免重複生成同一個數列，
可以運用陣列紀錄每一個起始 n 值對應的週期，
由於最大的週期是 525，
所以可以用 1000000 個 short int 的陣列，
這樣子會佔用 2MB 的記憶體，
這個大小的陣列可以定義成區域變數或是全域變數，
如果用一個迴圈計算這 1000000 個 n 領頭的數列的週期，
時間上會有一點浪費，
需要 0.7545 秒 (這些數據都不是絕對的，
但都是在同一台機器上測量的，
相對的比例會有參考性)，
主要是因為數列是用 3n+1 和 n/2 計算出來的，
如果在計算過程中發現數列第 m 項的週期 p 是先前曾經算出來的，
那麼現在這個數列的週期就是 p+m-1，
不需要一個一個數列從頭到尾產生出來，
同時一旦某一個 n 領頭的數列的週期 q 算出來以後，
2n 的週期就是 q+1，
4n 的週期就是 q+2，
...
這個建表的時間需要儘量縮減，
測試一下大概可以做到 0.02133 秒 (35 倍)。
這個建立表格的過程因為每一個工作是基於前面已經做好的部份工作，
雖然並沒有特別的最佳化目標 (要說這個序列是最短的應該也是對的)，
一般也稱為動態規劃 (Dynamic Programming)。
如果這裡用遞迴以及 memoization 來建表，
同樣也可以大量地減少重複的計算。
接下來需要面對的是「區間最大值查詢」的問題，
如果不做任何加速，
每次查詢陣列的第 i 個元素到第 j 個元素之間的最大值，
需要 j-i 次的比對，
以這個問題來說，
雖然陣列的內容是固定的，
但是查詢次數多而且範圍重複得很多的話會是一個相當大的負擔，
遇見這種問題通常會使用線段樹或是樹狀數組來加速，
如果陣列的內容是不斷變動的，
查詢最大值更需要使用這樣的資料處理方法。
前面我們看過「a693 吞食天地」
在做區間部份和的查詢，
陣列元素固定時部份和查詢可以運用前綴和來加速，
就不怕查詢會有很多重疊的部份，
那個時候我們也說如果陣列元素是動態變化的，
前綴和就幫不上太多忙了，
需要使用線段樹 (segment tree), 影片, 或是樹狀數組 (Binary Index Tree), 影片 的資料結構幫忙，
現在雖然陣列元素是固定的，
但是我們要求的是區間中的最大值，
還是需要藉由線段樹或是樹狀數組的幫忙，
才能夠省下重複比大小的動作。
實作上面講的幾種速度提昇方法，
對於自己生成的 500 個隨機查詢，
可以得到下列的數據：
不過想到像費氏序列 f(n) = f(n-1) + f(n-2)
如果直接用遞迴函式實作的話，
因為會用相同的參數重複呼叫很多次，
例如計算 f(6) 需要呼叫 f(5) 和 f(4),
計算 f(5) 時就重複呼叫 f(4) 了，
執行起來會非常慢，
需要用 memoization 的方法，
以陣列來紀錄過程中計算出來的數值，
避免用相同的參數重複呼叫。
回到我們這個問題，
需要代一些數值來分析一下這個函數到底有什麼性質，
例如根據題目的公式計算 f91(85) 如下：
不過再多試幾個數值看看，
根據題目的公式計算 f91(73) 如下：
在計算 f91(n), 0<=n<=91 函數值的時候，
需要計算 f91(n+11), f91(n+22), ...
這樣子一定會計算到 f91(m)=91, 91<=m<=101，
所以這個函數 f91(n), 0<=n<=100 的數值都是 91，
在 100<n 的時候是 n-10，
根本不需要寫遞迴函式，
多寫多錯，
直接用 if 敘述判斷一下就夠了，
是個唬人的遞迴公式呀！
現在這個問題是很接近的，
有兩種步伐：每步一階或是每步三階，
如果都沒有休息站，
其實就是計算滿足 f(n) = f(n-1) + f(n-3), f(0)=f(1)=f(2)=1 數列的 f(n) 值。
現在有休息站的情況下，
SF 在每一個休息站一定會停下來，
所以由一個休息站繼續往上爬的時候，
只有唯一的一種方式，
重新再根據上面的遞推公式計算到達下一個休息站有多少種爬法。
分段來看，
如果起點到第 1 個休息站有 n0 種爬法，
由第 1 個休息站到第 2 個休息站有 n1 種爬法，
。。。，
由第 m 個休息站到終點有 nm 種爬法，
那麼總共就有 n0 * n1 * ... * nm 種爬法。
注意 f(n) 這個數列增長得非常快，
計算的時候應該要使用 long long 的資料型態，
先前我們也看到如果用迴圈計算的話，
應該要用一個陣列來紀錄整個數列，
如果用遞迴方式來計算的話，
更是一定需要運用陣列來做 memoization，
因為每一段都會運用到同樣的數列，
所以紀錄起來的數值不需要重新計算，
計算乘積的時候數字增大得更快，
C/C++ 語言裡面基本的資料型態很快就紀錄不了這樣的數值，
如果超過了就會出現錯誤，
這種時候就需要用自己設計的方式來紀錄整數，
並且實作加減乘(除)的運算，
通常我們說這是大整數，
大整數其實在金融上是有需要，
在工程領域上大部份的應用都只需要科學記號，
可以容忍一定的誤差，
但是在資訊安全的應用中，
密碼系統會需要十進位 300~1000 位數的大整數。
這個問題需要根據一個影像的 DF-expression 表示方法以及影像的大小 n，
還原出影像的 nxn 個 0/1 像素 -- 解碼 DF-expression，
然後計算 1 像素的個數。
上圖 (a) 輸入是 (0,8)，
輸出是 0 個 1 (64 個 0)；
上圖 (b) 輸入是 (1,8)，
輸出是 64 個 1；
期末考
int i, b[32], x=123456789;
for (i=0; x>0; x/=2)
b[i++] = x%2;
while (--i>=0)
printf("%d", b[i]);
如果用遞迴函式由最低位開始來轉換 x 的進位制的話：
void conv(int x)
{
if (x==0) return;
conv(x/2);
printf("%d", x%2);
}
int w, x2, x=123456789;
for (w=1,x2=x; x2>1; x2/=2)
w *= 2;
for (; w>0; x%=w,w/=2)
printf("%d", x/w);
printf("\n");
a132 Parity
十進位轉二進位的過程中計算 1 的個數，
如果是奇數，
同位元就是 1，
否則就是 0。
這是所謂的偶同位元，
原來的二進位表示方法加上這個同位元以後，
一定是偶數個 1。
用一個 for 迴圈來實作如下：
for (count=0; x>0; x/=2)
count += x%2;
因為不需要列印出二進位的表示方法，
所以雖然這個迴圈是從最低位元開始計算，
還是可以正確得到位元總數。
e357 遞迴函數練習
就是很直接的遞迴函式。
b373 車廂重組
課堂中我們談到了氣泡排序法，
也會做一次 實習，
這個方法是一種藉由交換相鄰兩個順序不對的數字來完成排序的方法，
在這個練習裡，
你可以仔細思考一下對於任何一組資料來說，
究竟會需要做幾次的交換，
你可以參考一下「逆序對」的定義。
d562 山寨版磁力蜈蚣
範例輸入:
5
99 77 66 44 11
7
1 98 95 52 56 34 43
範例輸出:
99 77 66 44 11
11 44 66 77
77 66 44
44 66
66
1 98 95 52 56 34 43
43 34 56 52 95 98
98 95 52 56 34
34 56 52 95
95 52 56
56 52
52
輸入是 n 個 0 到 100 之間的整數，
0 < n < 100。
輸出的第一列就是輸入的數列，
其後每一列是去除前一列第一個元素同時反轉過來的數列。
第一列需要列印第 0 個元素開始往後 5 個，
第二列需要列印第 4 個元素開始往前 4 個，
第三列需要列印第 1 個元素開始往後 3 個，
第四列需要列印第 3 個元素開始往前 2 個，
第五列需要列印第 2 個元素開始往前 1 個，
如果有下一筆資料的話多印一個換列字元。
f072 家裡的後花園
這個問題也是陣列、迴圈、和條件判斷敘述的練習，
把輸入資料讀入陣列裡面以後，
因為在柵欄外面是不能種花的，
可以先從最前面開始往後處理看到的第一個 1 之前的 0，
把這些 0 改為 1，
再從最後面開始往前處理看到的第一個 1 之前的 0，
把這些 0 改為 1，
接下來可以從頭到尾找尋 9，
把前後兩個都改成 1 (這個步驟小心不要超過土地的範圍)，
最後從頭到尾計算陣列裡還有幾個 0 就是所要的答案。
f149 炸彈偵測器
練習二維陣列、兩層迴圈。
如題目所述，需要處理相鄰的炸彈偵測器，
標示為失去效用的偵測器，
以每一個偵測器為中心去檢查四周是否有偵測器，
如果有其它偵測器，
這個偵測器就失去作用，
需要標示這個偵測器為失去效用，
例如改為 6，
導致它失去作用的那個偵測器同時也失去效用，
可以一起標示起來，
每一個還有作用的偵測器都需要以自己為中心來檢查，
但是檢查四周的時候，
也許有些偵測器已經標示失去作用，
但還是會導致四周的偵測器失去作用，
所以需要檢查 >= 5。
如果某一個偵測器是有效的，
就要把它周圍的炸彈標示為偵測到的炸彈，
例如改為 2，
最後再統計被偵測到的炸彈以及沒有被偵測到的炸彈。
第八週
第九週
a022 迴文
可以練習使用陣列和迴圈來檢測迴文，
也可以練習用遞迴函式來檢測迴文。
e543 Palindromes
這一題是迴文檢測的延伸：
迴文字串的定義是順著看和倒過來看完全一樣 str[i]==str[n-1-i]
鏡像字串的定義是順著看是倒過來看時的鏡像 str[i]==mirror(str[n-1-i])
根據題目裡的表列，
撰寫一個回傳鏡像字元的函式 char mirror(char c)，
或是定義一個 '1'~'9'...'A'~'Z' 對應到鏡像字元的陣列：
const char *mirror="1SE Z 8 -------A 3 HIL JM O 2TUVWXY5";
如此就可以用 mirror[str[n-1-i]-'1'] 來得到鏡像字元，
注意上面這個字串在 '9'-'1' 到 'A'-'1' 之間多保留了 7 個不會用到的字元 '-'，
因為 ASCII 字元表中 '9' 到 'A' 之間有 7 個標點符號。
注意如果字串長度是奇數，
檢測迴文字串時最中間那個字元不需要檢測，
但是檢測鏡像字串時，
最中間那個字元需要檢測是不是對稱的。
b367 翻轉世界
題目對於「翻轉 180 度」沒有定義得很清楚，
實際上就是在平面上把一個矩陣順或逆時針轉 180 度：
001
100
011
轉 180 度會得到：
110
001
100
下面這個矩陣轉 180 度會得到完全一樣的矩陣：
110
010
011
題目要求判斷輸入的矩陣是否轉 180 度得到完全一樣的矩陣?
f290 德潤的大軍
練習運用二維陣列一體式地存放每個士兵的防禦力以及攻擊力，
這樣才能夠運用 qsort() 以及自行定義的 compare() 函式排序。
如果防禦力以及攻擊力分開來存放在兩個陣列裡面，
qsort() 函式就沒有辦法把一個士兵的資料看成一個整體來排序。
以後你會使用結構語法時，
就可以練習使用結構來組織一個士兵的防禦力以及攻擊力兩個資料，
同時也可以運用 qsort() 以及自行定義的 compare() 函式排序。
b511 換銅板
這是我們在課堂中談到枚舉 (enumeration) 方法的練習，
請參考 投影片裡介紹的思考方法，
進階的換銅板是一個動態規劃的問題。
第十週
h081 程式交易
這是一個模擬的題目，
需要弄清楚題目所描述的規則，
題目最後的提示裡對於兩組測資有詳細解釋。
簡單地說就是手上最多只能有一張股票，
一開始不管價格多少都要買進，
把買價記錄下來，
如果手中有股票同時價格高過 進價+D 時賣出，
把賣價記錄下來，
如果手中無股票同時價格低於 賣價-D 時買入，
資料結束時不論手中有無股票都印出交易的總利潤。
a915 二維點排序
與 「f290 德潤的大軍」 類似，
再一次練習使用 qsort 排序一個二維陣列表示的點集合，
每一個點座標有 x, y 兩個正整數需要看成一個整體，
定義一個比對函式 int compare(const void*, const void*)
來實現先比較 x 座標再比較 y 座標、
由小排到大的要求。
f302 沒有 0 的阿拉伯數字
這是一個 9 進位轉 10 進位的數字轉換，
請複習一下前面的練習 「a034 二進位制轉換」，
或是實習 「07-2: 判定可能的最小進位制」。
這個 9 進位用的 9 個符號是 {1,2,3,4,5,6,7,8,9}，
所表達的數值例如 a3a2a1a0
等效的十進位數值是
a3 93 + a2 92 +
a1 91 + a0 90
19
範例輸出一:
18
1*9+9=18
111
範例輸出二:
91
1*9*9+1*9+1=91
e208 Decoding
Run-length encoding 在影像編碼裡是很常使用的，
尤其是影像裡有一大片同樣顏色或是灰階的區域時，
用來完成無損的數據壓縮。
編碼的範例如：
AABBBBDAA ⇒ A2B4D1A2。
這個題目要求完成反向的解碼 (decoding)，
輸入的字串僅包含數字 [0-9] 和字母 [A-Z]，
輸出的字串僅包含字母 [A-Z]
3
A2B4D1A2
A12
A1B1C1D1
範例輸出:
Case 1: AABBBBDAA
Case 2: AAAAAAAAAAAA
Case 3: ABCD
d597 2. 便當的編號與配菜組合
這個練習可以由上課時投影片第 6 頁兩層的數數字迴圈開始，
修改一點點來去除基本數數字時重複的數字 (第 26 頁)，
當然也可以用遞迴的方式來實作 (第 9 頁和第 27 頁)，
注意題目要求的數字不大，
所以暴力直接列舉就可以；
另外題目有要求依照指定順序生成這些組合，
所以不能使用交換的方式來節省運算時間。
a524 手機之謎
這個練習可以由上課時投影片第 7 頁，第 11 頁，兩層的數數字迴圈開始修改，
或是從第 14 頁的遞迴程式開始，
修改成由大數到小，
或是仍燃油小數到大，
但是列印的時候印出與 n+1 的距離。
d471 0 與 1 的遊戲
這是標準的二進位數數字程式，
可以由上課時投影片第 6 頁兩層的數數字迴圈開始，
修改一點點就可以完成，
當然也可以用遞迴的方式來實作 (根本就是第 9 頁的程式)。
g276 魔王迷宮
這是一個模擬的題目，
請仔細閱讀題目的說明，
需要完全了解題目你撰寫的程式才會通過測試，
注意每個回合所有的魔王都會移動一次，
炸彈會把該回合所有停在那一格的魔王都炸掉，
同一格的多個炸彈會一起炸掉，
範例測資一也顯示如果魔王的 (s,t) 是 (0,0) 的話，
自己會被自己留下的炸彈炸掉。
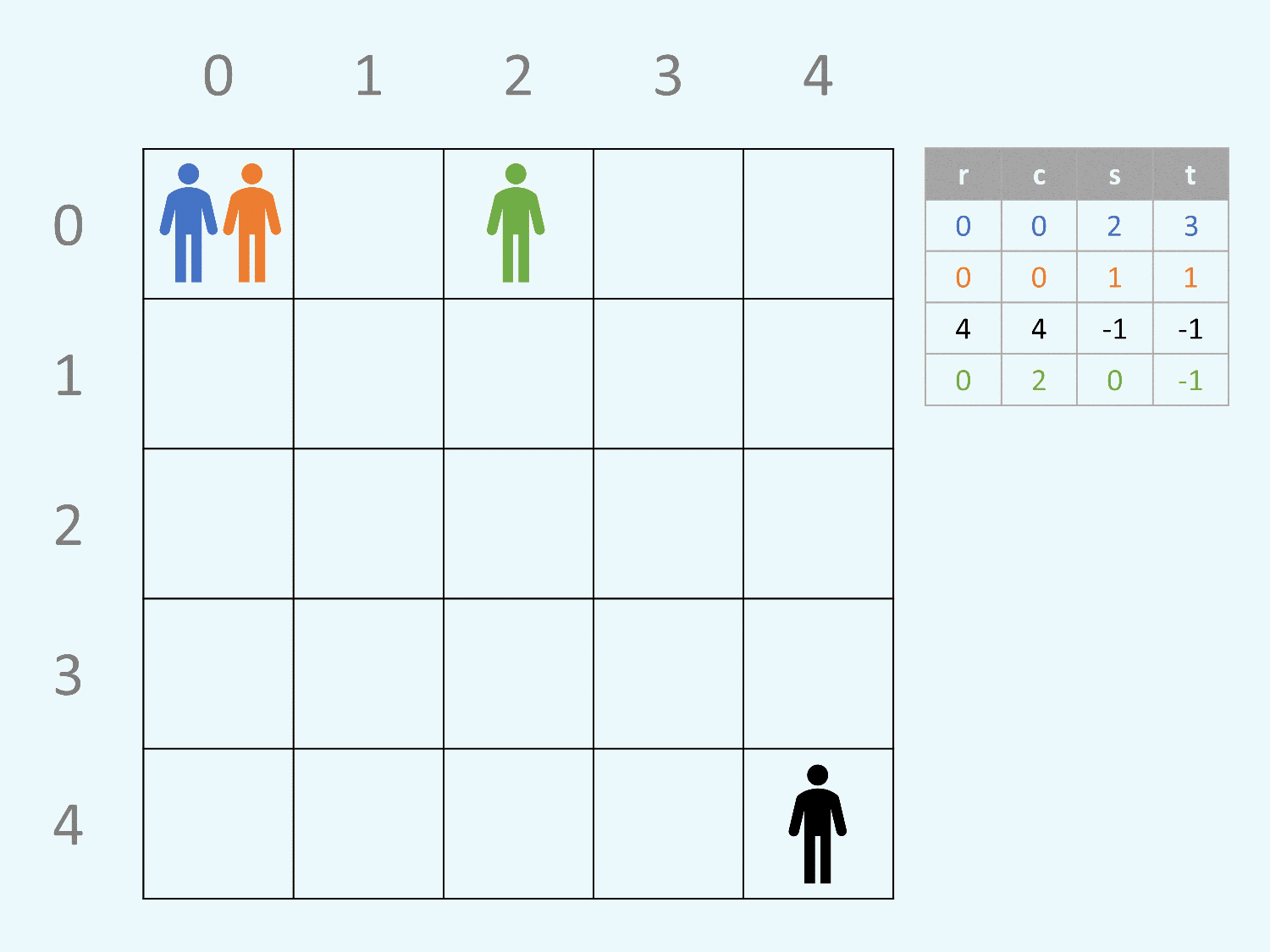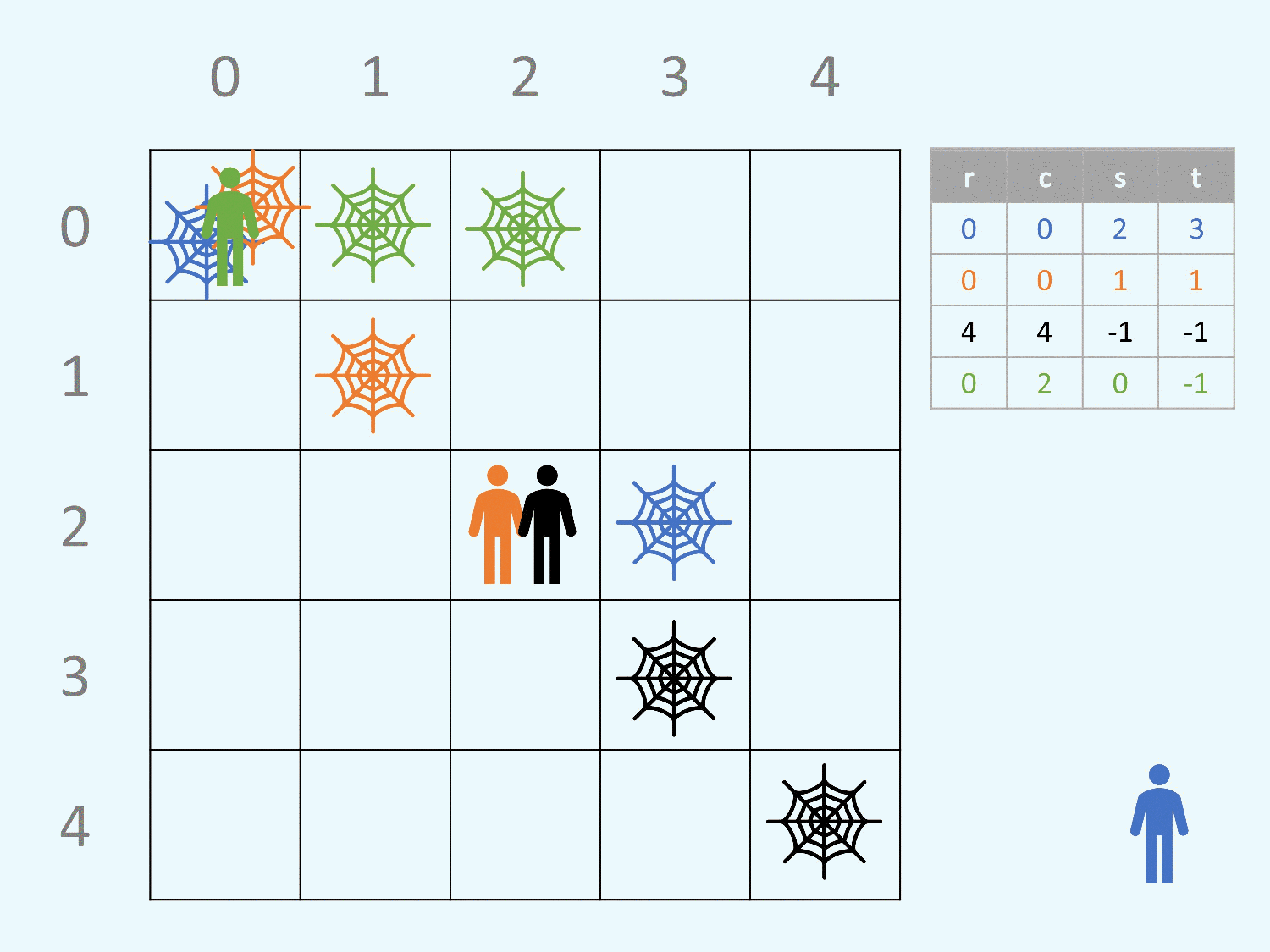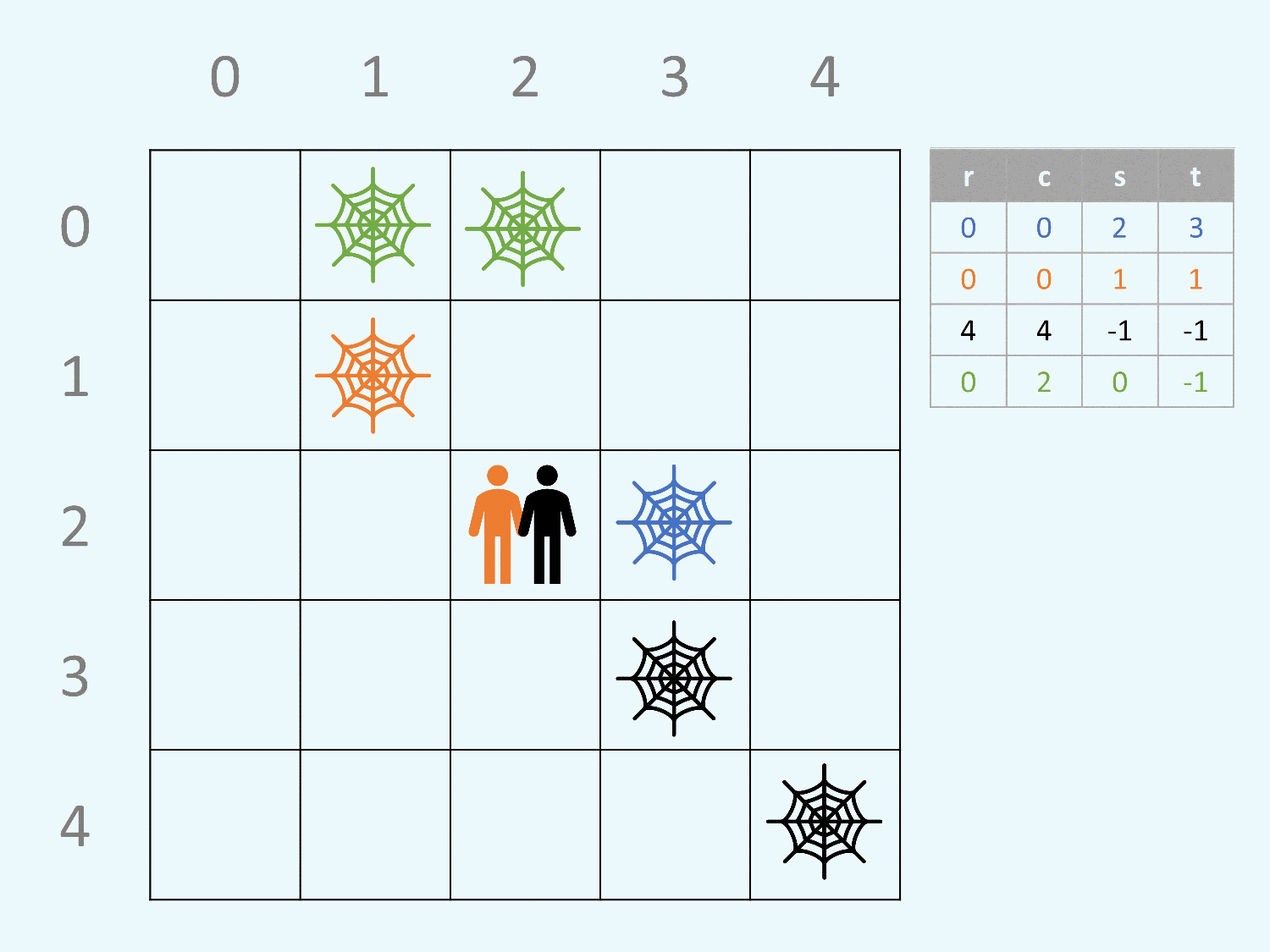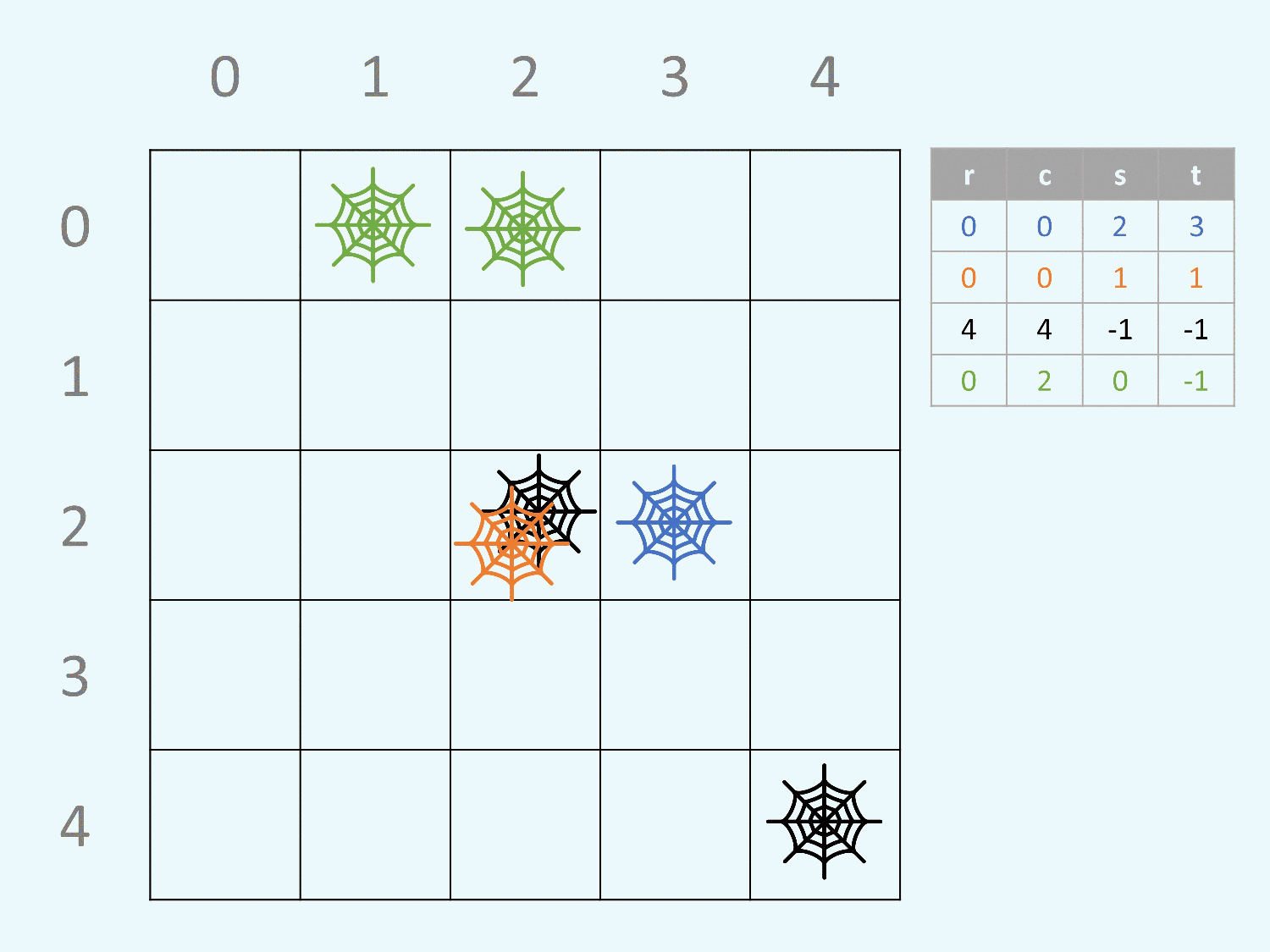
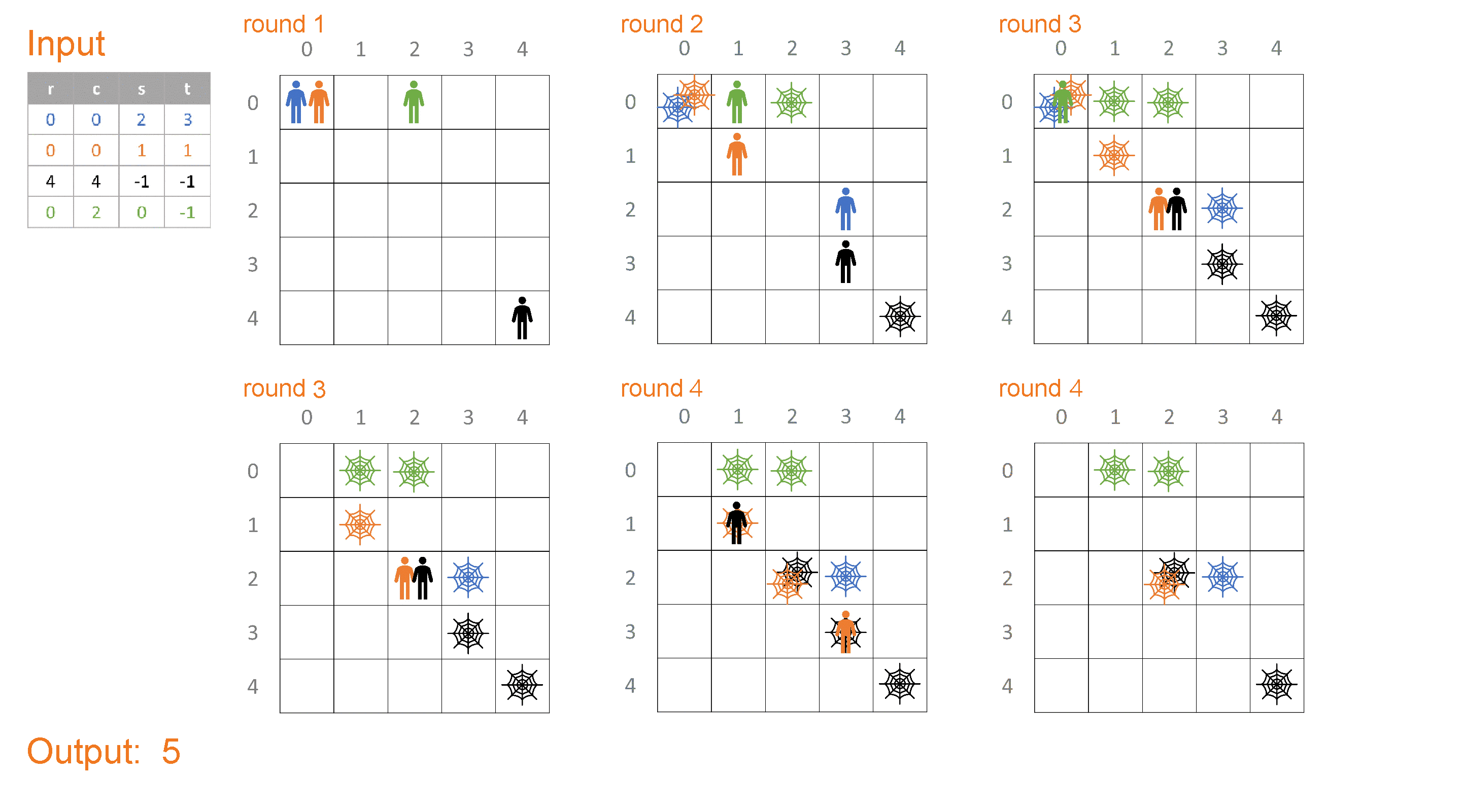
注意請注意讀題目，最後要輸出的答案是「有幾格有炸彈」，
不是「有幾個炸彈」。
e446 排列生成
產生 n 個數字的所有排列的方法很多種，
例如我們用數數字的迴圈或是遞迴方法，
用基於交換的遞迴方法，
用迴圈/遞迴的旋轉法，
或是用迴圈/遞迴的相鄰互換方法，
但是結果依照字典順序排列的只有兩種，
一種是數數字的方法，
另一種是基於交換的遞迴方法的變形。
d115 數字包牌
這個練習和前面「d597 便當的編號與配菜組合」用到的列舉方法幾乎相同，
可以由上課時投影片第 6 頁兩層的數數字迴圈開始，
修改一點點來去除基本數數字時重複的數字 (第 26 頁)，
當然也可以用遞迴的方式來實作 (第 9 頁和第 27 頁)，
題目要求的數字 m <=n<=100 其實很大，
照理說不是暴力列舉的問題，
但是題目要求輸出所有的組合，
如果測資裡面有像是 n=67, m=33 的話，
會有 264 種組合，
這要輸出在螢幕上可能需要很長很長的時間，
只能假設測資裡面沒有這麼大的了，
另外題目有要求依照指定順序生成這些組合，
所以不能使用交換的方式來節省運算時間。
第十一週
a251 假費波那契數
費氏序列是一個增加得很快的序列，
所以要評估一下需要使用的資料型態，
這個整數序列的計算公式是 Si = Si-4 + Si-1，
同時數列最前面的四項範圍在 0 到 5 之間，
序列最多有 20 項，
假如 S1 = S2 = S3 = S4 = 5，
到第 20 項才 1250 而已，
所以用 int 是綽綽有餘的。
f928 連環炸彈.................Bomb!
這一題還是模擬題，
把題目的描述看清楚，
炸彈分成三種：
Xi = 1 只會引爆自己，不會波及其他炸彈
Xi = 2 引爆自己後，會波及左右 Xi-1 和 Xi+1，總共兩個炸彈，
除非已經超出 0~N-1 的範圍
Xi = k, k≥3 引爆自己後，會波及左邊 Xi-k、Xi-2k
和 右邊 Xi+k、Xi+2k，總共四個炸彈，
除非已經超出 0~N-1 的範圍。 5
1 1 1 1 1
2
範例輸出#1:
1 1 0 1 1
模擬過程:
1 1 1 1 1
1 1 0 1 1
範例輸入#2:
5
1 1 2 1 1
2
範例輸出#2:
1 0 0 0 1
模擬過程:
1 1 2 1 1
1 0 0 0 1
範例輸入#3:
13
1 1 1 1 1 1 3 1 1 1 1 1 1
6
範例輸出#3:
0 1 1 0 1 1 0 1 1 0 1 1 0
模擬過程:
1 1 1 1 1 1 3 1 1 1 1 1 1
0 1 1 0 1 1 0 1 1 0 1 1 0
範例輸入#4:
13
1 1 1 1 1 1 3 1 1 2 1 1 1
6
範例輸出#4:
0 1 1 0 1 1 0 1 0 0 0 1 0
模擬過程:
1 1 1 1 1 1 3 1 1 2 1 1 1
0 1 1 0 1 1 0 1 1 0 1 1 0
0 1 1 0 1 1 0 1 0 0 0 1 0
b837 費氏數列
費氏數列 F(0) = 0, F(1)=1, F(n) = F(n-1) + F(n-2), n>=2，
也就是 0, 1, 1, 2, 3, 4, 13, 21, 34, 55, 89, 144, 233, 377,
610, 987, 1597, 2584, 4181, ..., F(30)=832040, F(31)=1346269
這個遞增數列，
題目要求找到在 A 和 B 之間(含) 有幾個 F(i)，
0<=A,B<j=1000000，
所以每一對輸入 A 和 B 之間最多有 31 個 F(i)，
只需要知道 A 和 B 在這個遞增數列的什麼位置就可以算出要求的個數，
如果寫一個迴圈由 F(1) 開始比對，
最多比 30 次，
平均起來可能比對 15 次，
查詢的數量 t 小於 10000，
所以每一個測資平均時間小於 300000，
直接寫迴圈應該會在 1 秒內 (大約 109個運算)。
int lower_bound(int x, int n, int data[]) {
int left=0, right=n-1, mid, result=n;
while (left<=right)
if (data[mid=(left+right)/2]>=x)
result = mid, right = mid-1;
else
left = mid+1;
return result;
}
如此每一次搜尋最多做 ceil(log30) 次比對，
所以平均的時間變成 2*5/2*10000，
大概是線性搜尋的 1/6。
h083 數位占卜
這個題目希望你練習一下字串處理、strcmp(), qsort(), 和 bsearch()，
直接看題目的例子，
兩支籤上的文字 piep 和 ie，
可以串接成 piepie
或是 iepiep，
不論是哪一種接法，
都可以拆分成兩個一樣的字串，
例如第一個接法是 piepie，
第二個接法是 iepiep，
這兩支籤稱為聖筊。
f145 肯尼的階乘位數
我們可以使用迴圈配合陣列來計算費氏序列 f(n)=f(n-1)+f(n-2), f(0)=0, f(1)=1，
也可以使用迴圈配合陣列來計算組合數 C(n,k) = C(n-1,k-1) + C(n-1,k), C(i,0)=1, C(i,i)=1，
前面這兩個例子裡可以看到如何運用序列中較小的數來計算後續的數。
現在這個例子裡再一次希望你能推導出遞推的公式，
使用迴圈配合陣列來計算序列中指定的數字。
這樣的計算是動態規劃演算法的基礎。
g(n) = f(n) * f(n-1) * ... * f(2) * f(1)
f(n) = n! * (n-1)! * ... * 2! * 1!
n! = n * (n-1) * ... * 2 * 1
n! 的位數是 1+floor(log n!) = 1+floor(log n + log n-1 + .... + log 2 + log 1)
f(n) 的位數是 1+floor(log f(n)) = 1+floor(log n! + log (n-1)! + ... + log 2! + log 1!)
g(n) 的位數是 1+floor(log g(n)) = 1+floor(log f(n) + log f(n-1) + ... + log f(2) + log f(1))
F(n) = F(n-1) + log n! = F(n-1) + E(n), F(1) = 0
G(n) = G(n-1) + log f(n) = G(n-1) + F(n), G(1) = F(1) = 0
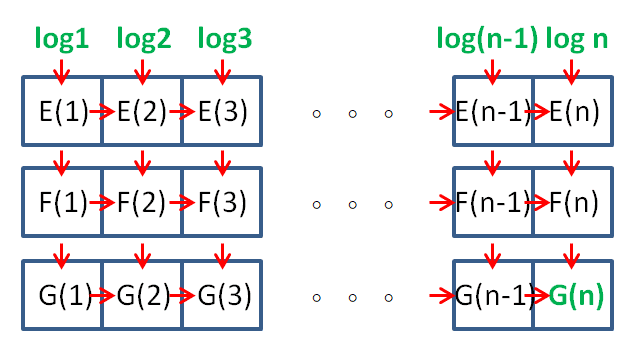
計算的時候可以用三個一維 n 個元素的陣列來算，
也可以用一個 3 列 n 行的二維陣列來存放，
不過仔細看運算的順序，
用一個一維 n 個元素的陣列其實就夠了，
記憶體是很珍貴的資源。
c531 基礎排序(偶數排序)
練習運用 qsort() 排序的題目很多，
qsort() 是以 n log n 的複雜度，
透過交換的方式排序 n 個同型態元素陣列的方法，
這個問題希望能夠練習間接地去存取要排序的資料陣列 data[]，
需要排序的資料可能散怖在 data[] 陣列中而沒有接續在一起，
但是運用一個陣列來間接存取並且排序這個中介的陣列是可以完成的，
基本上有兩種間接的存取方法：
int compare(const void *a, const void *b) {
return data[*(int*)a]-data[*(int*)b];
}
但是用這種方法時 data[] 陣列需要定義在全域的地方，
qsort() 函式在運作的時候，
傳遞進 compare() 函式的指標是指到 index[] 陣列內的元素，
並沒有辦法傳遞 data[] 陣列給 compare() 函式。
int compare(const void *a, const void *b) {
return **(int**)a-**(int**)b;
}
a158 Maximum GCD
題目看完以後覺得比起前面幾個遞迴問題都簡單，
計算 GCD 相對來講是簡單的演算法，
這題的通過比例只有 87%，
應該是因為由串流中讀入資料的時候，
以換列字元 \n 為分割點，
可能是這個阻礙了嘗試的人。
char buf[2];
int k;
for (k=0;;k++)
{
scanf("%*[ ]");
if (1==scanf("%[\n]", buf)) break;
scanf("%d", &a[k]);
}
來跳過串流內連續的空格，
讀取單一的換列字元，
如果成功就代表一列的結束，
如果失敗就表示這一個測資裡還有整數沒有讀入。
c471 物品堆疊 (Stacking)
雖然問題的描述看起來很複雜，
不過仔細推敲一下，
發現其實只要排序就可以解決，
請參考 投影片 的說明。
第十二週
e267 Group Reverse
範例輸入#1:
3 ABCEHSHSH
5 FAOETASINAHGRIONATWONOQAONARIO
0
範例輸出#1:
CBASHEHSH
ATEOAFGHANISTANOIRAQONOWOIRANO
ABC ⇒ CBA
EHS ⇒ SHE
HSH ⇒ HSH
最後輸出 CBASHEHSH。
i121 英文字母大小寫的抉擇
這一題有四種指定的規則來調整英文字的大小寫，
測資裡面會指定用哪一種規則，例如：
stop YELLING in Uppercase letters!
2
範例輸出#1:
STOP YELLING IN UPPERCASE LETTERS!
While (HUNGRY) eat(FOOD);
4
範例輸出#2:
while (hungry) eat(food);
1. 句首英文字母大寫，其它英文字母小寫：
i=0; while(p[i]<'A'||(p[i]>'Z'&&p[i]<'a')||p[i]>'z') i++; // 跳過所有空格與標點符號
if ((p[i]>='a')&&(p[i]<='z')) // 第一個字母如果是小寫則換成大寫
p[i] += 'A'-'a';
... // 一直到句尾如果是大寫字母就換成小寫 p[i] += 'a'-'A';
2. 全部英文字母大寫：由一開始一直到句尾如果是小寫字母就換成大寫 p[i] += 'A'-'a';
3. 每一個英文字的開頭需要大寫：
4. 全部英文字母小寫：
規則 3. 和 4. 基本上需要把所有大寫字母換成小寫，
然後規則 3. 額外需要檢查是不是每個英文字的第一個字母，
例如檢查 ((p[i]>='a')&&(p[i]<='z'))&&((p[i-1]<'a')||(p[i-1]>'z'))，
特別需要留意陣列的第一個元素，
可以設計一個從 -1 開始的陣列，
然後 p[-1]=' '; 來配合上面的檢查。
j124 石窟探險
仔細地閱讀程式的描述，
輸入其實是用 preorder (前序：父節點-子節點1-子節點2-。。。)
的順序把石窟的樹狀分支列印出來，
所以程式可以用遞迴的方式實作 preoder 的巡訪，
所讀入父節點石窟紀錄的編號 a 是奇數還是偶數就決定此節點的分支數，
進入一個迴圈執行 2/3 次遞迴函式的呼叫，
每次呼叫時可以傳入父節點紀錄的編號，
都巡訪完畢的時候，
資料可以順利地讀進程式裡，
然後在過程中根據傳入的參數計算父節點與子節點數值差異的和，
程式的要求就完成了。
2 6 0 8 14 0 0 0 10 0 4 0 0
範例輸出一:
26
這個輸入資料重建回樹狀架構時簡單表示如下：
2
6 10
0 8 0 4
14 0 0 0
0 0
2 是根節點，
6 和 10 是兩個子節點，
0 和 8 是 6 的兩個子節點，
0 和 4 是 10 的兩個子節點，
14 和 0 是 8 的兩個子節點，
0 和 0 是 14 的兩個子節點，
0 和 0 是 4 的兩個子節點。
輸出是 |2-6| + |6-8| + |8-14| + |2-10| + |10-4| = 26，
這個計算的順序就是 DFS 搜尋的順序。
5 2 10 0 0 0 8 0 0 17 0 0 0
範例輸出二:
26
這個輸入資料重建回樹狀架構時簡單表示如下：
5
2 8 17
10 0 0 0 0 0 0
0 0
5 是根節點，
2, 8 和 17 是 5 的三個子節點，
10 和 0 是 2 的兩個子節點，
0 和 0 是 8 的兩個子節點，
0, 0 和 0 是 17 的兩個子節點，
0 和 0 是 10 的兩個子節點。
輸出是 |5-2| + |2-10| + |5-8| + |5-17| = 26，
這個計算的順序就是 DFS 搜尋的順序。
b537 分數運算-1
這是一個很好的問題，
一開始看的時候有一點壓力，
覺得題目的描述很少，
不過逐步熟悉問題、
由分析範例的過程中突破是很重要的方法，
最後發現是一個遞迴問題的時候是很有趣的，
程式的實作短得可以，
遞迴的表達能力真的很好。
詳細請參考 投影片 裡面的問題分析過程。
c049 Square Pegs And Round Holes
問題的分析和解決問題的方法設計請參考
投影片 的說明。
稍微注意一下不需要把 (n-1)2 個點都測試完，
一行一行由 j=1 開始測試，
逐步增加 j，
但是一發現進入圓內就應該跳到下一行去，
至少可以節省 3/4 的時間。
d621 兔子跳鈴鐺
這一題是下一題「d304 複製貼上」的簡化版，
是一個標準的遞迴 DFS 問題，
比較奇特的是題目幾乎沒有說明，
而且通過率有 97%，
可能因為是一個遊戲相關的題目，
大家感覺特別親切吧。
做這一題之前當然要去看一下遊戲的：
網址，
選 GAMES 然後選第二列第一個鈴鐺。
遊戲中有一個鈴鐺分數的計數器，
內容由 1 開始，
兔子跳到鈴鐺時得到的分數就是這個計數器的數值，
每次跳鈴鐺得分以後計數器會增加 1，
另外跳到鴿子時目前總得分會乘 2、
鈴鐺分數的計數器則不會改變，
這個題目的輸入是一個 0 到 400 的一個整數，
如果這是遊戲的得分，
要求你寫一個程式來找出是跳到鈴鐺和鴿子的順序，
可能沒有答案 (請輸出 cheat!↵)，
也可能有多個答案，
例如題目輸入是 28 時，
1 * 2 + 2 + 3 * 2 * 2↵
的輸出代表遊戲中得到 28 分的計算方法，
也就是代表跳到 鈴鐺-鴿子-鈴鐺-鈴鐺-鴿子-鴿子，
注意這個加號乘號是即時計算的，
沒有依照先乘除後加減的。
1 + 2 + 3 + 4 + 5 + 6 + 7
1 + 2 + 3 * 2 * 2 + 4
是因為 "++++++" <
"++**+"。
d304 複製貼上
這個問題要找在編輯時最短的「複製」/「貼上」
動作序列來將一個 * 字元複製成指定數量的 * 字元，
例如可以用 Ctrl+C, Ctrl+V, Ctrl+C, Ctrl+V, Ctrl+V 由一個 * 字元複製成 6 個 * 字元，
注意這裡假設 Ctrl+C 是將所有字元複製到剪貼簿中，
另外不會有連續的兩次 Ctrl+C，
那樣子第二次的 Ctrl+C 是沒有意義的。
unsigned char masks[] = {0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80};
unsigned char imasks[] = {0xFE, 0xFD, 0xFB, 0xF7, 0xEF, 0xDF, 0xBF, 0x7F};
然後陣列定義為
char path[10005/8+3], minpath[6000][10005/8+3];
設定路徑上第 i 個動作為 0/1：
可以用位元運算 path[i/8] &= imask[i%8];
以及位元運算 path[i/8] |= mask[i%8];
來完成，
查看第 i 個動作可以用位元運算 path[i/8] & mask[i%8] != 0 來完成。
第十三週
f493 水窪問題
這個題目可以運用 DFS 來標示相同水窪區塊，
以下面的輸入為例來說明作法：
5 5
W#WWW
WW#W#
#W#WW
WWW#W
####W
這個 DFS 和老鼠走迷宮的 DFS 運作起來是非常接近的，
由任何一個點開始，
如果不是 'W' 或是不在 5x5 的區區域中就回傳 0，
如果是 'W' 的話，
就針對上下左右四個相鄰點遞迴呼叫去標示成 '$'、
計算並且回傳所標示的相連接 'W' 區塊的數量，
例如呼叫 dfs(0,0) 應該在遞迴之後回傳 7，
同時將所有相鄰的 'W' 標示為 '$'，也就是：
$#WWW
$$#W#
#$#WW
$$$#W
####W
只看單一一層的遞迴函式運作，
dfs(0,0) 會先把盤面標示為
$#WWW
WW#W#
#W#WW
WWW#W
####W
然後呼叫 dfs(0,1), dfs(1,0), dfs(0,-1), dfs(-1,-1)，
除了 dfs(1,0) 遞迴下去以後最終會回傳 6 之外，
其它三個呼叫都立刻回傳 0，
此相連接 'W' 區塊的數量則為 1 + dfs(0,1) +
dfs(1,0) + dfs(0,-1) + dfs(-1,-1) = 1 + dfs(1,0)。
接下來呼叫 dfs(1,0) 的時候除了把座標 1,0 的 'w' 換成 '$'，
也就是盤面標示為 $#WWW
$W#W#
#W#WW
WWW#W
####W
會遞迴呼叫 dfs(1,1), dfs(2,0), dfs(1,-1), dfs(0,0)，
此時除了 dfs(1,1) 遞迴下去以後最終會回傳 5 之外，
其它三個都立刻回傳 0，
如此就會一直遞迴到第 6 層，
也就是 dfs(2,1) - dfs(3,1) - dfs(3,0), dfs(3,2)，
一層一層的遞迴呼叫。
main() 函式裡對於 5x5 的每一個點都檢查是不是 'W'，
一發現是的時候就遞迴呼叫，
遞迴函式的結束條件是上下左右都沒有 'W'，
遞迴函式的主體包括
注意因為並不是像迷宮一樣尋找路徑，
在下層函式結束、退回來嘗試下一個方向之前，
不需要把該座標標示回 'W'，
如此才可以逐步標示整個盤面。
每接觸一區塊時就會藉由遞迴函式計算出相鄰 'W' 的數量，
把相鄰的這些 'W' 標示成 '$'，
這樣字就可以計算出總共有幾個水窪，
也可以算出水窪大小的最大值和最小值。
f640 函數運算式求值
這個題目要計算的東西可以由計算部份問題的結果進一步合成出來，
所以可以使用遞迴的方式來完成，
像先前的階乘計算，
計算 n! 可以分解成 n * (n-1)!。
int fcomb(int n, int x) {
if (n==1)
return f(x);
else
return f(fcomb(n-1,x));
}
其中函數複合的次數 n 設計成遞迴函式的參數，
函數的輸入 x 也設計成遞迴函式的參數。
int fcomb() {
int x;
if (1==scanf("%d", &x))
return x;
else
{
x=0, scanf(" f%n", &x);
if (x>0)
return f(fcomb());
else
printf("error in input stream\n");
}
}
再擴展到 f(x) 和 g(x,y) 一起的複合函式，
例如 f g f f 7 g 6 f 5，
是計算 f(g(f(f(7),g(6,f(5))))，
程式可以寫成
int comb() {
int x;
if (1==scanf("%d", &x))
return x;
else
{
x=0;
if (scanf("f%n", &x), x>0)
return f(comb());
else if (scanf("g%n", &x), x>0)
return g(comb(),comb());
else
printf("error in input stream\n");
}
}
如果不喜歡用 scanf 比對的功能，
也可以用 scanf("%c" 讀入字元：
int comb() {
int x; char ch;
if (1==scanf("%d", &x))
return x;
else
{
scanf("%c", &ch);
if (ch=='f')
return f(comb());
else if (ch=='g')
return g(comb(),comb());
else
printf("error in input stream\n");
}
}
h089 疊披薩
就是一個情境有點怪異的河內塔，
完全一樣的遞迴就可以完成。
可以練習一下不用遞迴、不用堆疊、
只用迴圈撰寫的河內塔，
請參考 投影片 36-39頁。
h206 強者就是要戰，但.....什麼才是強者呢？
這題在整個決策樹裡面不同層所比較的指標是不同的，
在遞迴函式的參數裡面一定需要包含層數，
參數還可以包含需要比對的資料個數，
在陣列中的起始索引值或是起始位址，
當資料個數為 1 時就停止不要遞迴下去，
遞迴主體中把資料分成兩半，
各自呼叫遞迴函式來得到勝出者的分數，
如果是奇數層則以大者勝出，
偶數層顛倒過來以小者勝出，
遞迴函式回傳勝出者的分數。
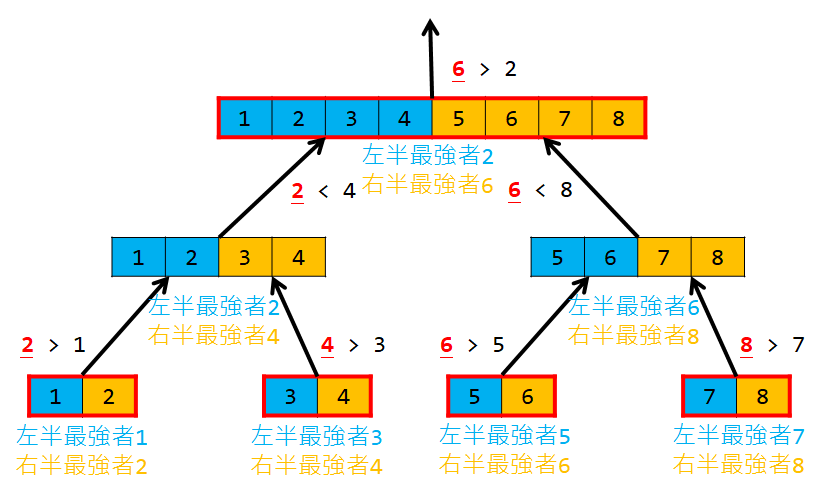
d576 辭典遊戲
遊戲規則:
1. 輪流從棋盤中取數字
2. 先下者只能從第一列中取數字 (先手由列中選取、後手由行中選取)
3. 前一位拿取數字的行或列，決定下一位取數的行或列
4. 取得數字總和較多者贏
題目裡面的範例對於遊戲規則說明得很清楚：
開始時棋盤上的分數：
1 2 3
4 5 6
7 8 9A 取第一列的 2
1 □ 3
4 5 6
7 8 9B 取第二行的 8
1 □ 3
4 5 6
7 □ 9A 取第三列的 9
1 □ 3
4 5 6
7 □ □B 取第三行的 3
1 □ □
4 5 6
7 □ □A 取第一列的 1
□ □ □
4 5 6
7 □ □B 取第一行的 7
□ □ □
4 5 6
□ □ □第三列已經被選完了，
A 沒得選，
遊戲結束。
兩個人輪流挑選作為決策，
每一次呼叫遞迴函式的時候，
兩個人各自有一個分數，
但是如果是奇數層，
就是第一個人被限制在某一列上挑選，
如果是偶數層，
就是第二個人被限制在某一行上挑選，
所以呼叫的參數需要包括
1. 兩人的分數，
2. 遞迴的深度 (沿著決策樹到達第幾層)，
3. 限制的列/行號。
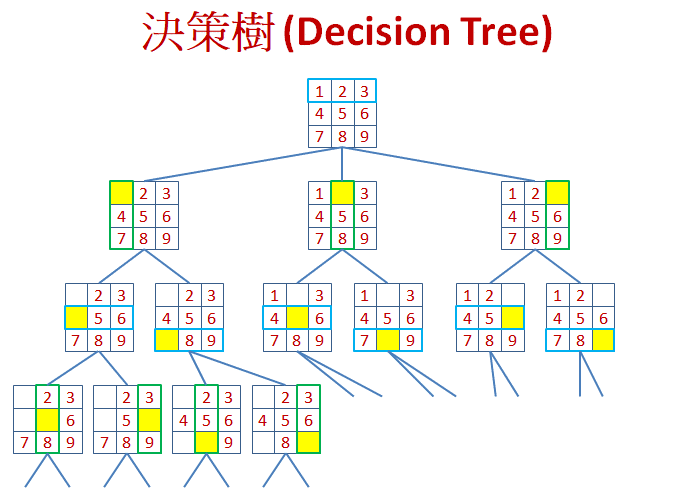
2. DFS 遞迴函式的主體 (有點像迴圈重複的主體) 就是進行那個決策點所有可能的選項，
在這個問題裡就是被限制的那一列/行上還剩下沒有被挑選的數字。
第十四週
e563 Meeting Room Arrangement
這個問題一開始看到的時候覺得有點複雜，
很多安排順序的問題都是時間複雜度很高的，
這個題目不需要用暴力列舉的方式來評估所有的活動組合，
因為這些活動的時間段是有順序的，
不論是開始的時間或是結束的時間，
活動時間有衝突也使得他們不能夠一起排入。
考慮所有的活動中最早結束的那個，
這個時間我們叫做 t，
我們一定可以讓它使用會議室，
不可能有其它的活動需要讓它讓出時段而使得有更多的活動可以舉行，
其它活動的結束時間都比 t 晚，
換成其它的只可能擋住更多的活動。
當然讓這個活動使用會議室以後，
所有活動起始時間早於 t 的都需要拒絕，
但是為了讓最多的活動可以舉行，
這個決定一定是最好的，
接下來考慮剩下所有起始時間大於 t 的活動，
還是找最早結束的那個活動，
所有的考量都再重複一次，
。。。
一直到沒有剩下任何活動為止。
c085 Pseudo-Random Numbers
在實習 10-2
仲夏夜之夢 裡面我們看過下面這個形式的虛擬亂數產生器：
Ln = ( Z * L + I ) mod M
它叫做線性同餘虛擬亂數產生器 (linear congruential pseudo random generator)，
這是非常常用的一個亂數產生器，
也是 stdlib 的 srand()/rand() 在使用的，
不同的系統上參數可能不太一樣，
但是都具有類似的特性，
就是統計上是均勻分佈的、
前後的關聯性低 (自相關係數接近 0)，
運用它可以模擬很多自然界中的物理現象，
不過只要知道 Z,I,M 三個數值，
它所生成的序列是完全可以預測的，
由連續生成的四個數值也可以解出 Z,I,M 的數值。
所以這個序列不能拿來取代真正的亂數，
不能拿來做資訊安全的應用，
不能拿來做線上遊戲、對奕、以及賭博。
c039 The 3n + 1 problem
這一題看起來困難度好像不高，
覺得就依照題目所說的一步一步進行，
很快就可以實作完成，
不過簡單測試一下就發現問題了，
第一是起始 n 值稍微大一點 (e.g. 159487) 就發現數列很快就超過 int 可以表示的範圍，
導致週期計算時的錯誤，
不過這個不是太大的問題，
換成 long long 就可以解決；
第二個是直接的實作執行起來相當花時間，
500 次隨機查詢區間內最大值就需要大約 100 秒，
我們的目標會在 0.05 秒，
大約 2000 倍的速度提昇，
至於該怎樣提昇速度呢?
應該是這個練習比較有挑戰的地方。
1. 直接模擬、不建表格 101.950 s
2. 迴圈建表、盡量不要重複產生數列 0.356 s
3. 遞迴建表 0.633 s
4. 迴圈建表 + BIT RMQ (range max query) 0.058 s
5. 迴圈建表 + 線段樹 RMQ 0.061 s
因為需要 線段樹 和 BIT 的應用非常多，
如果有機會的話，
了解一下這兩個機制並且實作一次。
c423 還原密碼
這個題目裡面需要用一個兩層迴圈計算 N-1 位元數字再加上一個未知位元數字 X 的根，
檢查根是否為指定的數字 R，
此時把位元 X 塞入 N-1 位元的數字可以得到 N 個不同的數字，
可能有不只一個 X 滿足上面的要求，
找出所有的可能性紀錄在一個二維的字元陣列裡，
再運用 strcmp() 以及 qsort() 排序以後，
去除重複的以後再去除最小和最大的，
由小到大依序列印出所有可能性。
c462 交錯字串 (Alternating Strings)
仔細看一下題目，
這個題目需要先計算有幾個連續的大寫字母、小寫字母，
根據這些數字，
判斷是否有 k 交錯字串，
最長的 k 交錯字串長度是多少，
對於這樣的問題，
可以試著用狀態圖來描述大寫小寫的組合：
請參考 投影片 的說明。
第十五週
c002 f91
這一題看起來就是一個直接的遞迴公式：
1. 如果 n <= 100, 則 f91(n) = f91(f91(n+11))
2. 如果 n >= 101, 則 f91(n) = n-10
想當然爾應該寫一個遞迴函式來實作。
f91(85) = f91(f91(96))
f91(96) = f91(f91(107)) = f91(97)
f91(97) = f91(f91(108)) = f91(98)
f91(98) = f91(f91(109)) = f91(99)
f91(99) = f91(f91(110)) = f91(100)
f91(100) = f91(f91(111)) = f91(101) = 91
根據題目的公式計算 f91(86) 如下：
f91(86) = f91(f91(97))
f91(97) = f91(f91(108)) = f91(98)
f91(98) = f91(f91(109)) = f91(99)
f91(99) = f91(f91(110)) = f91(100)
f91(100) = f91(f91(111)) = f91(101) = 91
果然發現如果直接照著題目給的遞推公式寫遞迴函式的話，
會以相同的參數 0~100 重複呼叫很多次，
所以如果要寫遞迴函式實作，
一定要做 memoization，
陣列只需要存放 f91(0), f91(1), ..., f91(100) 這 101 個元素就夠了。
f91(73) = f91(f91(84))
f91(84) = f91(f91(95))
f91(95) = f91(f91(106)) = f91(96)
f91(96) = f91(f91(107)) = f91(97)
。。。
f91(100) = f91(f91(111)) = f91(101) = 91
根據題目的公式計算 f91(91) 如下：
f91(91) = f91(f91(102)) = f91(92)
f91(92) = f91(f91(103)) = f91(93)
f91(93) = f91(f91(104)) = f91(94)
f91(94) = f91(f91(105)) = f91(95)
f91(95) = f91(f91(106)) = f91(96)
。。。
f91(100) = f91(f91(111)) = f91(101) = 91
根據題目的公式計算 f91(70) 如下：
f91(70) = f91(f91(81))
f91(81) = f91(f91(92))
f91(92) = f91(f91(103)) = f91(93)
。。。
f91(100) = f91(f91(111)) = f91(101) = 91
咦！都是 91 耶！
c560 SF 愛運動
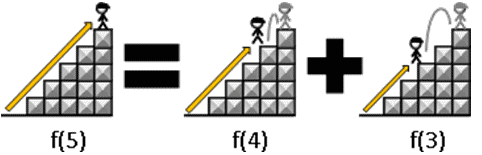
在講費氏序列的時候，
看過下圖的爬樓梯問題，
計算由地面開始爬到頂端有多少種不一樣的爬法，
f(n) = f(n-1) + f(n-2), f(0)=f(1)=1。
f637 DF-expression
題目裡 DF-express 的影像表示方法是用遞迴的方式來描述的：
編碼 nxn 的黑白影像時 (n=2k)
1. 如果每一格像素都是白色，我們用 0 來表示
2. 如果每一格像素都是黑色，我們用 1 來表示
3. 如果像素並非同色，均分為四個邊長 n/2 的小正方形，表示為 2 再接左上、右上、左下、右下四塊的編碼
題目要求輸入一個表示方法，
計算出影像中有幾個像素是 1。
下圖是編碼的範例：
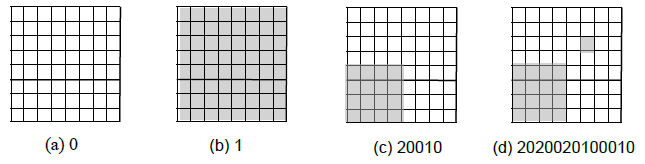
上圖 (c) 輸入是 (20010,8)，
因為第一位數是 2，
所以接下來要處理 4 個小的解碼問題，
輸入分別是 (0,4)，(0,4)，(1,4)，(0,4)，
輸出是分別 [0] 個 1，[0] 個 1，[16] 個 1，[0] 個 1，
最後把 4 個輸出加總 0+0+16+0=16，
輸出 [16] 個 1；
因為 DF-expression 越來越複雜了，
所以換成下面的符號表示，
每次在輸入看到 2 的時候，
需要處理 4 個邊長變成一半的解碼問題，
所以往右退四格：
(2,8)
(0,4) => [0]
(0,4) => [0]
(1,4) => [16]
(0,4) => [0]
+______
[16]
上圖 (d) 輸入是 (2020020100010,8)，
(2,8)
(0,4) => [0]
(2,4)
(0,2) => [0]
(0,2) => [0]
(2,2)
(0,1) => [0]
(1,1) => [1]
(0,1) => [0]
(0,1) => [0]
+______
[1]
(0,2) => [0]
+______
[1]
(1,4) => [16]
(0,4) => [0]
+______
[17]
手動解上面這四個例子時，
可以看到非常適合撰寫遞迴函式來處理，
這個函式接受邊長 n 作為參數，
回傳像素為 1 的個數，
n 為 1 的時候，
串流裡讀到的資料只會是 0 或 1，
只有一個像素不可能再分，
所以串流裡不可能是 2，
回傳的數值就是讀到的數值，
不會再繼續遞迴呼叫。
n 大於 1 的時候，
根據串流裡讀到的資料分別來處理四個子區塊：
串流裡讀到 0 的時候代表 n/2 x n/2 的 0 區塊，
串流裡讀到 1 的時候代表 n/2 x n/2 的 1 區塊，
串流裡讀到 2 的時候代表 n/2 x n/2 個像素裡有些是 0 也些是 1，
所以需要遞迴呼叫下去，
參數是 n/2，
回傳的數值就是這一個子區塊的 1 像素個數，
最後回傳出去的數值是四個子區塊 1 像素的總和。
c575 基地台
下圖中顯示的是五棟建築物的位置，
希望能夠找到適當的位置來設置 K 個基地台，
對於指定的 K，
請撰寫一個程式找到基地台需要具有的最小服務半徑，
能夠使這 K 個基地台滿足所有的建築物的需求。
請參考 投影片 的說明。
d443 Sweet Child Makes Trouble
請參考 投影片 的說明。
第十六週