| |
實 習 內 容 |
實
習
目
標 |
1. 靈活地運用函數來組織程式
2. 迴圈應用設計 |
1
|
二分勘根法
有的時候要你找一個方程式 f(x) = 0 的解時, 你沒有辦法寫出它的 closed-form 解, 例如 f(x) = x2
- 2 - cos(2 x) = 0. 這個時候我們可以用數值方法很快地去找到接近的 x 使得 f(x) 非常接近 0, 底下描述一個簡單的二分逼近法:
- 由一個可能的根的區間 [x1, x2] 開始, 也就是 x1, x2
滿足 f(x1) * f(x2) < 0
- 令 xleft = x1 且 xright = x2
- 然後測試 xleft 和 xright 的中間點 x3 = (xleft
+ xright) / 2, 如果 f(xleft) * f(x3)
< 0, 則令 xright = x3 (也就是搜尋的區間變成 [x1,
x3]), 否則令 xleft = x3 (也就是搜尋的區間變成 [x3,
x2])
- 接下去我們還是測試 xleft 和 xright 的中間點 x4
= (xleft + xright) / 2, 如果 f(xleft)
* f(x4) < 0, 令 xright = x4, 否則令
xleft = x4
- 如此不斷地重複
...
- xn = (xleft + xright) / 2, 如果 f(xleft)
* f(xn) < 0, xright = xn, 否則令 xleft
= xn ...
- 直到 f(xn) 是 0 或是 | xright - xleft
| < epsilon, epsilon 是一個指定的誤差值
上面說明中 xleft 和 xright 可以作為程式中的變數, xi
純粹是說明用的
以下圖片應該可以給你更多的直覺:
函數 x2 - 2 和 cos(2 x)
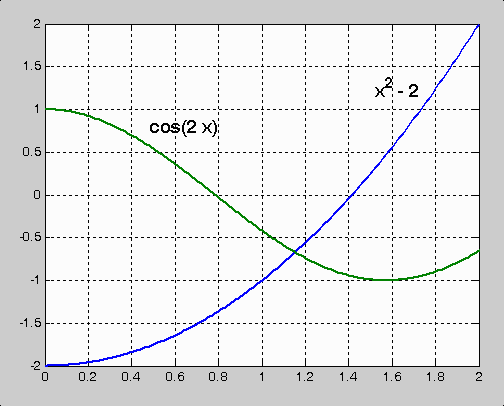
函數 f(x) = x2 - 2 - cos(2 x)

上圖中顯然根的範圍落在區間 [0, 2]. |
2
|
如何設計一個程式
(同時設計類似上面的演算法) 來得到接近的數值解?
第一步: 請你手動一步一步去做, 步驟越詳細越好,
不要遺漏任何步驟, 例如:
若 f(x) = x2 - 2 - cos(2 x)
- 由 xleft = x1 = 0 開始, f(xleft) =
-3, xright = x2 = 2, f(xright) = 2.6536,
f(xleft) * f(xright) < 0
- x3 = (xleft + xright) / 2 = (x1
+ x2) / 2 = 1, f(x3) = -0.5839, f(x3)
* f(xright) < 0, xleft = x3
- x4 = (xleft + xright) / 2 = (x3
+ x2) / 2 = 1.5 , f(x4) = 1.24, f(xleft)
* f(x4) < 0, xright = x4
- x5 = (xleft + xright) / 2 = (x3
+ x4) / 2 = 1.75 , f(x5) =1.999, f(xleft)
* f(x5) < 0, xright = x5
- x6 = (xleft + xright) / 2 = (x3
+ x5) / 2 = 1.375 , f(x6) =0.8149, f(xleft)
* f(x6) < 0, xright = x6
- x7 = (xleft + xright) / 2 = (x3
+ x6) / 2 = 1.1875, f(x7) =0.1304, f(xleft)
* f(x7) < 0, xright = x7
- x8 = (xleft + xright) / 2 = (x3
+ x7) / 2 = 1.0938, f(x8) =-0.2252, f(x8)
* f(xright) < 0, xleft = x8
- x9 = (xleft + xright) / 2 = (x8
+ x7) / 2 = 1.1406, f(x9) = -0.0469, f(x9)
* f(xright) < 0, xleft = x9
- x10 = (xleft + xright) / 2 = (x9
+ x7) / 2 = ...
在上面的步驟裡, 你可以注意到兩個步驟的差異很小, 常常這就是可以用 迴圈 來實作的地方,
在轉換成程式之前你需要把這些動作規律化, 你希望兩個步驟間重複的部份越多越好
第二步: 由上面手動計算過程中擷取
兩個步驟重複的共通部份 來得到 迴圈的主體
xi = (xleft + xright) / 2 = 1.75
, f(xi) =1.999,
如果 f(xleft) * f(xi) < 0 則 xright=
xi否則如果 f(xi) * f(xright) < 0 則 xleft=
xi
在運作過程中這些 xi 其實不需要是不同的變數, 在計算 xi+1 的時候, xi已經記錄在
xleft 或是 xright變數中了, 所以可以用單一的變數 xmid來存放
xi 的數值, 直接用 xi+1 覆蓋 xi 的數值就好了
第三步:
迴圈初始化
令 xleft = x1= 0 及 xright = x2=
2
第四步:
迴圈控制變數更新
if f(xleft) * f(xi) < 0 則 xleft
不變且 xright = xi
f(xi) * f(xright) < 0 則
xleft = xi 且 xright
不變
第五步:
迴圈結束條件
1. | f(xi) | <= 10-13 (在有限的有效位數下測試 f(xi)
== 0, 如果用 float 來設計的話就只能測試 | f(xi) | <= 10-7)
2. 或是 | xleft - xright | < epsilon (請注意, 因為是二分逼近法,
所以迴圈執行 n 次以後, | xleft - xright | 應該是 | x1
- x2 | * 2-n, 是一個可以預測的數值, 所以也可以由 | x1
- x2 | 以及可以接受的誤差 epsilon 先算出迴圈需要執行的次數 n)
請注意上面這兩個測試對於一個平滑的曲線來說是很接近的, 因為目標是 x, 所以比較常使用第 2 個
|
3
|
範例執行程式 (尋找 f(x)
= x2 - 2 - cos(2 x) 在 [0,2] 區間中的根)
基於上面的分析, 撰寫下列 bisect 函數
double bisect(double x_left, /* input - endpoints of interval in */
double x_right, /* which to look for a root */
double epsilon) /* input - error tolerance */
函數回傳 x 值使得 f(x) 的數值在 [-epsilon, epsilon] 區間中.
迴圈初始化:
x_left 是左邊的邊界, x_right 是右邊的邊界
x_mid = (x_left + x_right) / 2;
f_mid = f(x_mid);
f_left = f(x_left);
f_right = f(x_right);
迴圈結束條件設立:
while (fabs(f_mid) > 1e-13) 或是 (x_right - x_left
> epsilon) 或是先計算出迴圈需要執行的次數 n, 用 for (i=0; i<n; i++)
迴圈主體:
x_mid = (x_left + x_right) / 2;
f_mid = f(x_mid);
迴圈控制條件修改:
if (f_mid * f_left < 0)
{
x_right = x_mid;
f_right = f_mid;
}
else if (f_mid * f_right < 0)
{
x_left = x_mid;
f_left = f_mid;
}
請完成下列函式:
double bisect(double x_left, /* input - endpoints of interval in */
double x_right, /* which to look for a root */
double epsilon) /* input - error tolerance */
{
...
}
|
4
|
進一步的程式修改
我們可以把每次迴圈執行過程的 x_left, x_right, x_mid, 和 f_mid 都列印在螢幕上, 如此可以快速地看到程式是否表現正常
我們可以把條件測試 (x_right - x_left < epsilon)
放進迴圈裡面, 並且設定一個表示狀態的變數 root_found
如果條件滿足, 我們列印出成功的訊息, 否則列印出下一個區間 [x_left, x_right]
我們可以移除不需要的條件測試 (f_mid * f_right < 0)
甚至移除不需要的變數 f_right |
5
|
我們可以把想要求根的函數 f(x) 寫成一個 C 的函數:
double f(double x)
{
return x * x - 2 - cos(2 * x);
}
|
6
|
測試 bisect() 的 main() 函數如下:
#include <stdio.h>
#include <stdlib.h>
int main(void)
{
double epsilon, /* error tolerance */
root;
/* Get error tolerance from user */
printf("\nEnter tolerance> ");
scanf("%lf", &epsilon);
root = bisect(0, 2, epsilon);
printf("\n (%.7f)^2 + 2 = cos(2 * %.7f)\n", root, root);
system("pause");
return(0);
}
|
7
|
線上繳交版本請參考下列說明:
- 程式輸入四個倍精準浮點數 a, b, c, d 以指定多項式 f(x) = a
x2 + b x + c - cos(d x)
- 程式再輸入一個倍精準浮點數 epsilon 以指定根 r 的函數值 f(r)
距離 0 的可以容忍的誤差範圍 [-epsilon, epsilon]
- 程式再輸入兩個倍精準浮點數 x1 及 x2 代表根的範圍 (假設範圍內一定有一解)
- 程式印出 r 的數值 (小數點後請印 5 位數)
範例執行程式 |
![]()
![]()
