1
|
運用 while 迴圈設計 find_gcd() 函數
此函數可以運用 歐幾里得(Euclidean) 演算法 (輾轉相除法) 找到任意兩個正整數 n1 及 n2 的最大公因數
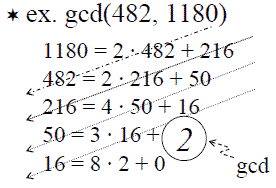
歐幾里得演算法:
- 將變數 q 設為變數 n1 內容的絕對值,
將變數 p 設為變數 n2 內容的絕對值
- 將 q 除以 p 的餘數設為 r
- 當 r 大於 0 時
3.1 拷貝 p 的數值至 q
3.2 拷貝 r 的數值至 p
3.3 將 q 除以 p 的餘數設為 r
- p 即為 n1 和
n2 的最大公因數
設計 C 程式實作歐幾里得演算法:
- 函式名稱、函式參數、函式回傳值: 這個函式需要得到兩個 int 型態整數, 最後算出一個 int 型態的正整數最大公因數
int find_gcd(int n1, int n2)
- 宣告函式內區域性 int 型態變數 p, q, r (此處變數的名稱配合演算法裡變數的名稱, 不另外取名字了)
- 設計 while 迴圈的基本步驟:
a. 迴圈控制變數初始化
b. 迴圈結束條件
c. 迴圈控制變數的更新
d. 迴圈主體
- 迴圈控制變數初始化:
運用 stdlib.h 函數庫中的 int abs(int) 函數來計算整數 n1, n2 的絕對值
q = abs(n1); p = abs(n2);
求 q 除以 p 的餘數 r:
r = q % p;
- 迴圈結束條件:
r != 0
- 此處迴圈主體和迴圈控制變數是結合在一起的:
q = p;
p = r;
r = q % p;
- 迴圈結束時 p 的數值即為最大公因數, 函數回傳 p 作為執行的結果:
return p;
|
![]()
![]()
