這是第一個和 C++ 物件化相關的作業, 所以我的說明比較多, 另外這個作業和實習裡的複數類別的設計也有很多相似點, 按部就班地作應該不會太困難, 雖然這比較像一個習題, 挑戰性稍微少了一點, 不過還是可以練習許多必備的 C++ 語法與程式設計, 事實上要寫的東西很多, 會遇見的錯誤也絕對無法預期, 請提早寫, 否則一定寫不完。
這三個學分的課程中作業佔的比例很高, 在我的認知裡如果你不幸考試考得不好, 但是你能夠說服我作業和實習的題目自己可以完成, 那我就沒有理由當你, 但是如果你考試成績不佳, 作業缺交或是抄襲, 那就很難讓你過, 主要的目的是希望你不是只會紙上談兵, 只看得懂部份的程式, 只會修改程式、但是卻不會設計程式, 很多時候軟體系統的運作原理是和程式設計習習相關的, 不會設計程式, 你就很難體會軟體系統的運作方法、長處與限制。
千萬不要放棄這些作業, 萬一最後你只完成了部份, 還是建議你連同設計還有偵錯時的心得一起交過來, 唯一不需要交過來的是別人的作業 (由這次作業開始, 作業是要 demo 的, 一直到期末你看到成績之前, 如果發現某次作業是抄襲的, 作業的成績還是會追回的), 如果你撰寫時遇見問題, 歡迎你隨時找我或是助教詢問, 上課後, 上課前, 實習課, 電話, email, msn... 都可以運用, 當然這也是說服我 - 你的確付出努力去完成這個作業 - 最直接的辦法。
請下載範例執行程式 1.exe 並請參考執行結果 (未完成)
實數的連續分數 (Continuous Fraction)表示法：
任何一個有理數 p/q 都可以表示成唯一的連續分數,
例如
,
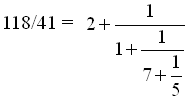
其中每一個分數的分子都固定是 1
我們可以簡寫為 118/41 = [2;1,7,5]。
再舉一個有理數的例子 12345/729 = 4115/243 = [16;1,14,5,2,1]。
同樣的, 一個無理數也可以用唯一的連續分數表示, 但是分母會有無限多項,
例如
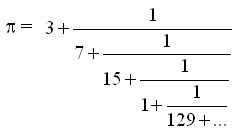
= [3;7,15,1,292,...]。
這種連續分數的表示法和十進位表示法一樣, 在表示一個實數的時候可能是有限位數或是無限位數, 比較不太一樣的是用十進位表示時有些有理數也可能需要無限位數才能精確地表示出來, 例如 1/3; 用十進位表示時無理數都需要無限且不出現循環的位數來表示。
使用連續分數來表示的話, 有理數一定是有限位數, 無理數的連續分數表示法一定有無窮多項。
很多無理數的連續分數表示會出現循環,例如 21/2 = [1;2,2,2,....] = [1;(2)], 上式中我們用 (2) 代表 2,2,... 的循環; 另外例如 31/2 = [1;1,2,1,2,1,2,....] = [1;(1,2)], 上式中我們用 (1,2) 代表 1,2,1,2,.... 的循環; 或如 311/2 = [5;(1,1,3,5,3,1,1,10)]
請注意因為一個無理數的連續分數表示法一定有無窮多項,
如果只取有限項的話,
一定小於所要表達的無理數,例如 
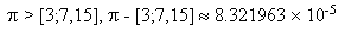
根據上面的定義和特性描述，請撰寫程式完成下列功能
在這個作業中我們希望製作一個 "連續分數" 的類別, 這種類別的物件可以代表一個正的實數 (有理數或是無理數)。
對於一個這樣子型態的物件來說, 必須提供一些基本的功能, 例如: 加法, 乘法, 倒數, 相等, 設定, 列印, 拷貝 等等功能, 請製作一個 "ContinuousFraction" 的類別來處理這樣的資料。
詳細功能要求如下:
物件內部存放資料時, 請存放 [a; b, c, d, ...] 格式, 由於需要考慮存放無理數, 所以你也要設計能夠表示有幾位數字的循環, 由於有一些無理數不會循環, 你也需要設計一個精確度上限來存放該數字的近似值, 內部資料請使用標準 C++ 函式庫裡的 vector 鬃來存放資料。
這兩個成員函式需要把傳進來的資料轉變為內部資料的存放格式, 其中第一個版本函式的參數是分子 p 以及分母 q (代表 p / q), 第二個版本有三個參數, 第一個參數 digits[] 是整數陣列, 內容為 [a; b, c, d, ...] 格式, nDigits 代表 digits[] 陣列中數字的個數, 第三個參數是為了表示出現循環而用的, 代表 digits[] 陣列中最後幾個數字出現循環, 例如表示 31/2 = [1;1,2,1,2,1,2,....] = [1;(1,2)] 時, digits[] = {1, 1, 2}, nDigits = 3, nPeriod = 2, 第三個參數 nPeriod 請使用預設參數, 資料請設為 0, 代表預設沒有循環, 請注意如果原先一個物件內有舊的資料的話, 必須先清除掉, 如果設定失敗的話, 應該要傳回 false, 反之成功的話就傳回 true, 這兩個成員函式是 public 的界面函式。
例如 number.setSquareValue(41.0, 15); 代表希望把 number 這個 ContinuousFraction 的物件的數值設為 411/2, 如果連續分數沒有辦法精確表示的話, 用 15 個數字來近似。
請注意在這個運算裡不論是傳入的物件或是自己這個物件的內容維持不變, 請用 const 語法保證這 兩件 事情。
請特別注意如果傳入的物件根本就是自己這個物件的話, 要傳回 true 的結果, 有了這樣的設計也一定要在 unitTest() 函式中加入適當的測試。 請使用 this 指標來檢查傳入的物件是否等於自己。
ContinousFraction::unitTest();請注意在 demo 程式的時候一定會要求你執行單元測試, 如果你沒有寫, 或是你的單元測試裡沒有替每一個功能設想可能的使用方法, 沒有設計測試的資料 (測試資料是你在撰寫每一部份的功能時都需要隨時思考的), 助教就不知道要看些什麼, 你的作業成績就不好了。
這個函式會讀取傳入的 original 物件內的資料, 並且拷貝到自己這個物件內, 如果自己這個物件內原先有資料的話, 需要先清除然後再拷貝。
請注意在這個運算裡不論是傳入的物件或是自己這個物件的內容維持不變, 請用 const 語法保證這 兩件 事情。
請特別注意如果傳入的物件根本就是自己這個物件的話, 要傳回 false 的結果。
ContinuousFraction x;
ofstream outfile("TestOutput.txt");
...
cout << x;
outfile << x;
ContinuousFraction x; ... cin >> x;
a. setValues() 界面
b. 加法
c. 乘法
d. 大於
e. 等於
f. 拷貝
g. 輸出到一個暫時的檔案
h. 由檔案中讀資料回來
如果你在設計這個類別的過程裡有撰寫其它輔助用的成員函式的話,
也應該在這裡對每一個功能加上測試的程式碼。
請由鍵盤讀入三個數字 n1=[a; b, c, d], n2=[e; f, g, h], n3=p/q
將此三個數字存放在 ContinuousFraction 類別的物件裡
請利用 ContinuousFraction 的功能來計算下列運算式
(n1 + n2 ) * n3
並且將結果以 p/q 格式以及 [a; b, c, d] 格式列印在螢幕上
原則上你想要增加什麼功能都是可以的, 記得在心得中寫出來, 這樣我才會注意到, 也才能夠幫你加一些分數, 現在程式還簡單, 你應該有辦法增加功能或是基於這個類別做一些好玩的應用。
回
C++ 程式設計課程
首頁
製作日期: 03/17/2008
by 丁培毅 (Pei-yih Ting)
E-mail: pyting@cs.ntou.edu.tw
TEL: 02 24622192x6615
國立台灣海洋大學
電機資訊學院
資訊工程系
Lagoon
