Lab 9-1: CComplex 的應用與 Mandelbrot 圖形界面

| 實習目標 |
使用實習 3-1, 4-2 中的CComplex 類別
做一個 Mandelbrot 碎形圖形 練習與基本圖形界面的合作 練習視窗界面程式的 debug |
|---|---|
| 步驟一 |
請執行 Mandelbrot02a 程式
這個程式會顯示 Mandelbrot 碎形圖形如下圖: 

int i, j;
Complex c;
double step = range / (windowSize-1);
for (i=0; i<windowSize; i++)
for (j=0; j<windowSize; j++)
c = Complex(centerX-range/2.0+i*step,
centerY+range/2.0-j*step);
上面迴圈中每一次算出來的複數 c 就是每個座標點 (i, j) 所對應的複數值。
接下來我們需要測試繪圖區域內每一個點, 看看在下列的測試公式下, 每一個 c 值發散的狀況:
令複數 z 的初始值為 0+0i
令每一個點的複數座標為 c
重複計算
z = z * z + c
每次運算後, 如果 z 的實部或是虛部絕對值超過 2
的話, 就表示已經發散掉了, 此時請記錄由開始到
發散需要計算上式幾次, 通常在前 50 次計算中,
會發散的點就已經有百分之九十九都發散掉了,
剩下的也幾乎不會發散了
上圖中同一顏色的那些點代表它們都在算到相同次數時發散掉的 (超過 2/-2 的)
上面是一個很漂亮的圖形, 而且如果放大來看的話, 它會不斷重複類似的圖案, 請執行 Mandelbrot03a, 在自然界中這種圖形很多, 這種圖形也常常可以用簡單的數學公式描述出來 如果發散的條件改成 "當 z 的實部和虛部的絕對值都超過 2" 的話, 還是一個碎形圖形, 但是看起來感覺不太一樣: 
|
| 步驟二 | 請下載圖形界面程式碼 Mandelbrot02b.rar, 解壓縮出來, 請編譯並且執行, 你應該可以看到視窗中是全部空白的, 選單中有 檔案/MaxIteration 設定的選項, 我們將在這個 project 中應用你先前寫的 CComplex 類別來撰寫程式 |
| 步驟三 |
首先在 ClassView 中你可以找到 Mandelbrot 類別,
打開這個類別你可以看到下列類別的定義以及空的成員函式:
class Mandelbrot
{
public:
Mandelbrot(double centerX, double centerY, double range);
void generateData(int ** &data,
int windowSize,
int maxIterations);
void deleteData(int ** &data, int windowSize);
private:
...
};
首先建構元函式會傳進來繪圖中心點的複數平面的座標,
例如 (-0.5, 0), 以及繪圖區域的寬與高 (目前所畫的是一個方形區域),
例如 2.3,
請在 Mandelbrot 類別中用資料成員記錄下來
|
| 步驟四 |
void generateData(int ** &data, int windowSize, int maxIterations);
這個成員函式應該要檢查傳入的指標, 如果是 0 的話, 動態配置一塊二維的整數 (int) 陣列, 其架構如下圖 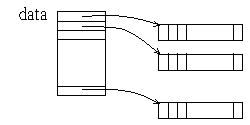
|
| 步驟五 |
這個 data 陣列的每一點代表繪圖區域中一個像素 (pixel),
依照一般的慣例,
data[0][0] 代表左上角, data[0][windowSize-1] 代表右上角,
data[windowSize-1][0] 代表左下角, data[windowSize-1][windowSize-1] 代表右下角,
你需要計算那個點的複數座標,
依照步驟一中的公式算算看在做到第幾次時 z 的實部或是虛部的絕對值超過 2,
然後記錄在 data[i][j] 中,
請注意傳入的 maxIterations 數值是你在測試時的最大次數
在你真正去算 z 的運算式並且算出 data[i][j] 之前, 你可以先把 data[i][j] 設定成一些簡單的圖樣來測試一下, 例如 (直紋):
for (i=0; i<windowSize; i++)
for (j=0; j<windowSize; j++)
data[i][j] = i%256; |
| 步驟六 |
上面步驟中你需要用到一個 CComplex 的複數類別,
同時類別中要有
CComplex add(CComplex &rhs);
CComplex multiply(CComplex &rhs);
兩個成員函式,
這兩個成員函式我們在前面的實習中定義過,
不過那時定義的是 add(CComplex &rhs) 實際上是 addEqual(CComplex &rhs),
也就是把 rhs 的數字和自己這個物件加起來,
並且修改自己這個物件的內容,
你可以直接用上次的成員函式來實作 z = z * z + c, 例如
z.multiplyEqual(z);
z.addEqual(c)
或者你也可以修改你的函式 addEqual() 為 add(),
讓它在把兩個數字加起來以後,
不要修改自己那個物件,
而是以傳值 (call by value) 的方式把一個 CComplex
的物件傳回,
如此你在實作 z = z * z + c 時需要用類似下列敘述:
z = c.add(z.multiply(z));
或是
tmp = z.multiply(z);
z = tmp.add(c);
請注意如果你直接將前面實習的 Complex.cpp 和 Complex.h 拷貝進來的話,
請在你的 Complex.cpp 檔案的第一列加入 #include "stdafx.h"
如此 compiler 才不會跟你抱怨說它找不到 pch 檔案
|
| 步驟七 |
void deleteData(int ** &data, int windowSize);
函式中需要實作將步驟四中配置的二維陣列刪除的程式碼 此時你可以編譯並且執行, 畫面上應該可以看到 Mandelbrot 的顯示了, |
| 步驟八 |
如果程式不幸出錯或是沒有顯示的話...就只好開始 debug 了,
這個程式是視窗的界面, 所以你沒有辦法用 cout, cin
來偵錯, 當然你可以用 VC 的 source debugger 一步一步執行來找錯誤,
不過這是最慢的方法, 同時在過程中你也會看到一大堆根本不是你寫的程式...
很困擾呢...
在使用 Microsoft Foundation Class (MFC) 製作視窗界面時, 我們常用一個 TRACE 巨集來取代 cout, TRACE 的用法和 printf 很像, 相信你還沒有忘記怎樣用 printf, 例如:
TRACE("m_data=%d\n", m_data);
TRACE("m_doubleData=%f\n", m_doubleData);
這些敘述的輸出會到哪裡去呢?
如果你用 debug 模式執行的話, 會跑到 output 視窗中, 如果你是正常執行的話, 可以開啟 dbwin32 程式來顯示偵錯的結果 |
| 步驟九 |
請測試一下選單 檔案/MaxIterations 設定,
當使用者更改過這個設定值 (10-120) 後,
你提供的 generateData 會重新被呼叫到,
同時 maxIterations 參數會有新的數值傳入
由於你在這個程式中有動態配置記憶體, 請特別在 dbwin32 視窗中確定一下程式結束時有沒有 memory leakage |
| 步驟十 | 請將所完成的 project (去掉 debug/ 資料匣下的所有內容) 壓縮起來儲存在 cyber 上你的帳號內, 後面的實習課程可能需要使用這裡所完成的程式 |
