|
就是下面這個 C 程式了 (希望你沒有什麼程式恐懼症,它看起來比較長、有點討厭的原因應該是為了實作比較有效率的資料結構的關係,不過是程式而已,程式做的工作多,人需要做的工作就少,生活就愉快一點!)
#include <stdio.h>
#include <malloc.h> // malloc(), free()
struct Entry
{
int row;
int col;
int value;
};
void printMatrix(struct Entry matrix[]);
void transposeMatrix(const struct Entry A[], struct Entry B[]);
void multiplyMatrix(const struct Entry A[], const struct Entry B[], struct Entry C[]);
int main()
{
int i;
struct Entry A[100]={0}, At[100]={0}, B[100]={0}, Bt[100]={0}, C[100]={0};
scanf("%d%d%d", &(A[0].row), &(A[0].col), &(A[0].value));
for (i=1; i<=A[0].value; i++)
scanf("%d%d%d", &(A[i].row), &(A[i].col), &(A[i].value));
A[i].row = -1; // extra entry for multiplyMatrix()
scanf("%d%d%d", &(B[0].row), &(B[0].col), &(B[0].value));
for (i=1; i<=B[0].value; i++)
scanf("%d%d%d", &(B[i].row), &(B[i].col), &(B[i].value));
B[i].row = -1; // extra entry for multiplyMatrix()
if ((A[0].row != B[0].row)||(A[0].col != B[0].col))
{
printf("Matrix A and B are not of the same dimension!\n");
return 1;
}
printf("\n");
printf("Matrix A:\n");
printMatrix(A);
printf("Matrix B:\n");
printMatrix(B);
transposeMatrix(B, Bt);
printf("Transpose Matrix B:\n");
printMatrix(Bt);
multiplyMatrix(A, Bt, C);
printf("Matrix A * Matrix B':\n");
printMatrix(C);
transposeMatrix(A, At);
printf("Transpose Matrix A:\n");
printMatrix(At);
multiplyMatrix(At, B, C);
printf("Matrix A' * Matrix B:\n");
printMatrix(C);
getchar(); getchar();
return 0;
}
void printMatrix(struct Entry matrix[])
{
int i;
printf("%d * %d matrix with %d non-zero item:\n",
matrix[0].row, matrix[0].col, matrix[0].value);
for (i=1; i<=matrix[0].value; i++)
printf("<%d,%d:%d>\n", matrix[i].row, matrix[i].col, matrix[i].value);
printf("====================\n");
}
void transposeMatrix(const struct Entry A[], struct Entry B[])
{
int i, iB=0, *start = (int *) malloc(sizeof(int)*(A[0].col+1));
B[iB].row = A[0].col; B[iB].col = A[0].row; B[iB++].value = A[0].value;
for (start[0]=1, i=1; i<=A[0].col; i++)
start[i] = 0;
for (i=1; i<=A[0].value; i++)
start[A[i].col+1]++; // counting element's in a row
for (i=1; i<=A[0].col; i++)
start[i] += start[i-1]; // accumulating
for (i=1; i<=A[0].value; i++)
{
iB = start[A[i].col]++;
B[iB].row = A[i].col;
B[iB].col = A[i].row;
B[iB].value = A[i].value;
}
free(start);
B[B[0].value+1].row = -1; // extra entry for multiply to test end of B1's row
}
void multiplyMatrix(const struct Entry A[], const struct Entry B[],
struct Entry C[])
{
int iA, iC, iA1, iB1, iA1row, iB1row, sum;
struct Entry *B1 = (struct Entry *)
malloc(sizeof(struct Entry)*(B[0].value+2));
transposeMatrix(B, B1);
C[0].row = A[0].row;
C[0].col = B[0].col;
C[0].value = 0;
iA = iC = 1;
while (iA <= A[0].value)
{
sum = 0;
iA1 = iA; iB1 = 1;
iA1row = A[iA1].row; iB1row = B1[iB1].row;
while (iB1 <= B1[0].value)
{
if (A[iA1].col == B1[iB1].col)
{
sum += A[iA1].value * B1[iB1].value;
iA1++; iB1++;
}
else if (A[iA1].col > B1[iB1].col)
iB1++;
else // if (A[iA1].col < B1[iB1].col)
iA1++;
if (A[iA1].row != iA1row)
while (B1[iB1].row == iB1row) iB1++;
if (B1[iB1].row != iB1row)
{
if (iB1 <= B1[0].value)
iA1 = iA;
else
while (A[iA1].row == iA1row) iA1++;
if (sum!=0)
{
C[0].value++;
C[iC].row = iA1row;
C[iC].col = iB1row;
C[iC++].value = sum;
sum = 0;
}
iB1row = B1[iB1].row;
}
}
iA = iA1;
}
free(B1);
}
|
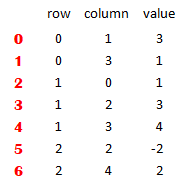
輸入測試資料
3 5 7
0 1 3
0 3 1
1 0 1
1 2 3
1 3 4
2 2 -2
2 4 2
3 5 7
0 0 3
0 1 1
1 0 -1
1 3 2
2 0 5
2 1 2
2 4 -1 程式輸出結果
Matrix A:
3 * 5 matrix with 7 non-zero item:
<0,1:3>
<0,3:1>
<1,0:1>
<1,2:3>
<1,3:4>
<2,2:-2>
<2,4:2>
====================
Matrix B:
3 * 5 matrix with 7 non-zero item:
<0,0:3>
<0,1:1>
<1,0:-1>
<1,3:2>
<2,0:5>
<2,1:2>
<2,4:-1>
====================
Transpose Matrix B:
5 * 3 matrix with 7 non-zero item:
<0,0:3>
<0,1:-1>
<0,2:5>
<1,0:1>
<1,2:2>
<3,1:2>
<4,2:-1>
====================
Matrix A * Matrix B':
3 * 3 matrix with 7 non-zero item:
<0,0:3>
<0,1:2>
<0,2:6>
<1,0:3>
<1,1:7>
<1,2:5>
<2,2:-2>
====================
Transpose Matrix A:
5 * 3 matrix with 7 non-zero item:
<0,1:1>
<1,0:3>
<2,1:3>
<2,2:-2>
<3,0:1>
<3,1:4>
<4,2:2>
====================
Matrix A' * Matrix B:
5 * 5 matrix with 14 non-zero item:
<0,0:-1>
<0,3:2>
<1,0:9>
<1,1:3>
<2,0:-13>
<2,1:-4>
<2,3:6>
<2,4:2>
<3,0:-1>
<3,1:1>
<3,3:8>
<4,0:10>
<4,1:4>
<4,4:-2>
====================
下面是這次考試的詳細要求 |
|
考試時間:
110分鐘 (11:10
截止上傳,為了避免截止時間系統以及網路的延遲,請提早 10 分鐘上傳,確保你已經上傳一個版本了)
- 請使用 Visual
Studio 2010 新增專案,讓 Visual Studio 為方案建立目錄,設定方案名稱是
quiz1,(專案)名稱為
C_Version,加入一個
C++ 程式檔案 main.cpp,將上述程式拷貝進去,編譯執行,複製貼上前面的輸入資料,測試一下程式輸出是不是和上面一樣
- 請將 main 函式裡面讀取矩陣的程式段落寫成一個
readMatrix 函式,下面是 main 函式裡讀取矩陣
A 的程式段落
scanf("%d%d%d", &(A[0].row), &(A[0].col), &(A[0].value));
for (i=1; i<=A[0].value; i++)
scanf("%d%d%d", &(A[i].row), &(A[i].col), &(A[i].value));
請設計好函式的參數,將 main 函式裡面由鍵盤讀取矩陣 A 以及讀取矩陣 B 的程式段落用 readMatrix(A); readMatrix(B);
取代,請使用 iostream 函式庫取代 stdio 函式庫,請編譯並且測試
請注意 A[i].row = -1; // extra entry for multiplyMatrix() 不要放進 readMatrix
裡面,這一列是額外為了配合 multiplyMatrix 演算法的,但是 i 需要改成什麼呢? 你稍微看一下讀資料的程式碼就知道應該是
A[0].value+1
- 測試的時候用眼睛檢查輸出真的不是好辦法,請撰寫一個 int
equalMatrix(const struct Entry A[], const struct Entry B)
函式來比較兩個矩陣是不是完全相等,相等回傳 1,不等回傳 0;然後把
main 函式裡面運用 transposeMatrix 計算的結果 BT
和下面的 C0 代表的稀疏矩陣比較,把運用
multiplyMatrix 計算 A
和 BT 相乘的矩陣和下面這個
C1 代表的稀疏矩陣比較,把運用 multiplyMatrix
計算AT
和 B 相乘的矩陣和下面這個 C2
代表的稀疏矩陣比較,運用 assert
以及 equalMatrix 確認相乘的結果是對的,請編譯並且測試
struct Entry C0[] = {{5,3,7},{0,0,3},{0,1,-1},{0,2,5},{1,0,1},{1,2,2},{3,1,2},{4,2,-1}};
struct Entry C1[] = {{3,3,7},{0,0,3},{0,1,2},{0,2,6},{1,0,3},{1,1,7},{1,2,5},{2,2,-2}};
struct Entry C2[] = {{5,5,14}, {0,0,-1},{0,3,2},{1,0,9},{1,1,3},{2,0,-13},
{2,1,-4},{2,3,6},{2,4,2},{3,0,-1},{3,1,1},
{3,3,8},{4,0,10},{4,1,4},{4,4,-2}};
- 在 transposeMatrix 函式裡有一個動態配置的 start 陣列,這個陣列用來暫時存放原本矩陣每一行有幾個元素,也就是轉置過的矩陣每一列有幾個元素,在最後面執行轉置動作的迴圈裡,直接把每一個元素放到新矩陣中正確的位置去,用完以後就釋放掉了,請使用
vector 類別的物件來取代這個陣列,請編譯並且測試
- 在 multiplyMatrix 函式裡有一個動態配置的陣列 B1,這個陣列是暫時存放轉置的矩陣
BT 的,請運用
new[]/delete[] 的語法取代 malloc/free
(其實這裡也可以和上一步驟一樣用 vector 來取代),請編譯並且測試
C 程式的部份到此告一段落,接下來是 C++ 的部份
- 請點選方案總管,以滑鼠右鍵點選「方案 'quiz1' (1 專案)」,在右鍵選單中選擇「加入/新增專案」,在
quiz1 方案中新增一個專案,名稱是 CPP_Version,在方案總管或是類別總管中以右鍵點選
CPP_Version,選擇「設定為起始專案」(如下圖,你會看到起始專案的名字變成粗黑字,後面步驟裡建置和執行程式才是執行這個 CPP_Version
專案裡面的 main() 函式,如果起始專案還是 C_Version,建置和執行程式時就一直是執行 C_Version 裡面的 main()
函式)
- 上面的 C 程式裡用一個陣列來存放稀疏矩陣的所有資料,但是單看這些資料也可能是描述 N
個城市的座標,並不能夠明確代表一個稀疏矩陣,接下來請製作一個 SparseMatrix
類別,這個類別的物件需要能夠描述一個稀疏矩陣,上面的 struct Entry
的定義還是需要的,在類別裡需要有四個私有資料成員
, m_nRows, m_nCols, m_nElems 是三個整數分別存放稀疏矩陣有幾列、有幾行、有幾個非 0 的元素,struct
Entry 指標 m_A 裡面運用 new[] 動態配置的 m_nElems+2 個 struct Entry 元素 (多出兩個元素,第一個元素
m_A[0] 是完全沒有用到的,只是因為原本程式的陣列侍從 A[1] 開始放資料,考試時間不夠,多一個元素的話可以不要修改原本的程式裡陣列使用時的註標,另外最後多一個元素也是配合原來的
multiplyMatrix 裡面的演算法的),Visual Studio 會替你多定義兩個 SparseMatrix() 建構元函式和
~SparseMatrix() 解構元函式 (我們還沒有解釋這兩個成員函式,但是它們很重要,先保留不要刪除它們)
- 接下來需要製作 read,
equal, print,
transpose, 和 multiply
這五個成員函式 (請注意 C 版本函式的名稱都是 xxxMatrix 來和其它功能的函式區分開來,但是
C++ 版本定義在 SparseMatrix 類別裡,本來就不會和其它功能的函式混淆,所以名字裡的 Matrix 可以都拿掉了,例如
void printMatrix(struct Entry matrix[]) 函式改為 void print()),另外函式的參數也需要修改,因為成員函式執行時都有一個目標的稀疏矩陣物件,矩陣物件收到
print 訊息時就是列印自己這個物件,不需要再傳入其它參數了,一開始這裡會有點混亂,程式一次改太多、改太急、又沒有逐步測試的話,很容易就把原本程式的機制改錯了,以下給你一些步驟提示,就當作重新設計這個類別的功能,逐步設計並且測試每一個實作出來的功能
- 首先請在 SparseMatrix 類別裡製作一個 static 的 void unitTest()
成員函式,把剛才步驟 1,2,3,4,5 改好的 C_Version 版本的 main() 函式裡的內容拷貝進來,但是請先註解掉這些程式,另外新增一個
main.cpp,裡面有一個 main() 函式,函式裡呼叫這個 unitTest(),編譯、確定可以執行 (確定執行的是這個新的
main() 函式)
- 在 unitTest 函式裡面原本有存放稀疏矩陣的 Entry 結構陣列 A, At,
B, Bt, C,初始化為 0,現在先改成 SparseMatrix 類別的物件,但是因為類別裡有成員函式,已經沒有辦法用 C 風格的
= {0} 來初始化了,請製作一個 SparseMatrix 類別的成員函式 void setValue(int
nRows, int nCols, int nElems, struct Entry *A),函式裡將對應的成員設定為傳入的參數值,並且在定義完稀疏矩陣
A 物件後呼叫 A.setValue(0,0,0,0) 來初始化 A 物件,請定義並初始化其它 At, B, Bt 幾個物件,接下來的
C0, C1 和 C2 物件也是類似的方法處理,請把 unitTest 後面還沒改到的程式註解起來,編譯並且測試
- readMatrix(A); 需要改成傳送 read
訊息給物件 A,也就是 A.read();
請在 SparseMatrix 類別裡新增 void read() 成員函式,由
C 版本的函式 void readMatrix(struct Entry matrix[]) 的內容拷貝進來,主要需要改的是沒有參數矩陣
matrix 了,你需要把資料讀進自己這個物件的資料成員 m_nRows, m_nCols, m_nElems, ... 裡面,另外請運用
new[] 配置 m_A 陣列,配置前請先刪除原本的 m_A 陣列,請把 unitTest 後面還沒改到的程式註解起來,編譯並且測試
- unitTest 函式中接下來有個條件判斷敘述 if ((A[0].row != B[0].row)||(A[0].col
!= B[0].col)
因為 unitTest 是 SparseMatrix 類別的成員函式,所以可以直接存取類別的私有資料成員,這裡只需要改一下資料成員的名稱就可以了,請把
unitTest 後面還沒改到的程式註解起來,編譯並且測試
- unitTest 函式中接下來是 printMatrix(A) 和 printMatrix(B),請修改為傳送訊息
print 給物件 A 和物件 B
請在 SparseMatrix 類別裡新增 void print() const
成員函式,拷貝 printMatrix 函式的內容進來,修改方法類似 read 成員函式,修改完成後請把
unitTest 後面還沒改到的程式註解起來,編譯並且測試
- unitTest 函式中接下來是 transposeMatrix(B, Bt),請修改為傳送訊息
transpose 給物件 Bt,以物件 B 為訊息的參數 (因為物件裡面有很大的陣列,為了避免拷貝,這個參數請用常數的參考變數),這樣設計的原因和前幾個函式製作時的原因是一致的
請在 SparseMatrix 類別裡新增 transpose 成員函式,拷貝 transposeMatrix 函式的內容進來,請注意轉置以後的矩陣要放在自己這個物件裡,其它部份的修改主要就是配置正確大小的
m_A 陣列,原本轉置矩陣的欄位 B[i].row, B[i].col, B[i].value 改為自己這個物件的成員 m_A[i].row,
m_A[i].col, m_A[i].value,原本 B[0].row, B[0].col, B[0].value 改為 m_nRows,
m_nCols, m_nElems,原本 A 矩陣的 A[i].row, A[i].col, A[i].value 改為 A 矩陣的資料成員
A.m_A[i].row, A.m_A[i].col, A.m_A[i].value,原本 A[0].row, A[0].col,
A[0].value 改為 A.m_nRows, A.m_nCols, A.m_nElems,在這個函式裡用的 vector,用完以後不需要特別去刪除,會自動完成清除的動作,修改完成後請把
unitTest 後面還沒改到的程式註解起來,編譯並且測試
- unitTest 函式中接下來是自動測試矩陣轉置結果是否正確的 assert 敘述,需要在
SparseMatrix 類別裡新增 bool equal(const
SparseMatrix &B) const 成員函式,拷貝 equalMatrix 函式的內容進來,修改方法類似
read 成員函式,修改完成後請把 unitTest 後面還沒改到的程式註解起來,編譯並且測試
- unitTest 函式中接下來是運用 multiplyMatrix(A, Bt, C)
以及 multiplyMatrix(At, B, C) 去計算 A
BT 以及 AT
B,並且和 C1,
C2 兩個預設的矩陣比較,(請注意由於一個
SparseMatrix 類別的物件中有動態配置的記憶體,使得我們不能夠運用 D = E; 這樣的語法來拷貝物件 E 的內容到物件
D,詳細原因以及解決的方法需要再過幾個星期才會講到),所以成員函式 multiply
需要設計配合 A.multiply(Bt) 的使用方法,也就是 void multiply(const
SparseMatrix &Bt),讓矩陣 A 乘上矩陣 Bt,乘積
A BT
直接放在矩陣 A 中,也就是矩陣 A 的內容在 A.multiply(Bt) 之後會改變,由於 unitTest 函式計算完 A
BT 之後還需要計算
AT
B,所以矩陣 A 如果在計算 A
BT 時會改變的話,AT
就需要在計算 A BT
之前先呼叫 transpose 計算出來,如此就可以順利測試完兩個稀疏矩陣的相乘,修改的重點應該只是角色的改變: 原本的矩陣 A 變成物件自己,原本的矩陣
Bt 還在,原本的矩陣乘積放在 C 裡面,在這個版本裡並不需要 C,但是乘出來的矩陣元素還是需要放在一個暫存的陣列中,這個陣列有可能是
0 個元素也有可能是 M * L 個元素,其實運用 vector<Entry> 非常適合,最後再將內容拷貝回物件自己的成員
m_A 中,然後是陣列元素 A[0].row, A[0].col, A[0].value, A[i].row, A[i].col,
A[i].value 變成成員 m_nRows, m_nCols, m_nElems, m_A[i].row, m_A[i].col,
m_A[i].value,不要更動演算法的話,程式比較不會出錯,請編譯並且測試。
[請注意:如果這一小題你覺得需要比較多時間,先完成其它部份的要求]
|