1042 Quiz#1 互斥集合 (Disjoint Sets)

C++ 實習測試: 1042 Quiz#1 互斥集合 (Disjoint Sets)

令集合 S 為整數 0 到 n-1 的集合，「互斥集合 (disjoint-sets)」資料結構 (或稱為「不相交集合」, 也稱為 union-find 資料結構, 或是 merge-find 資料結構) 的定義如下：

一個 disjoint-sets 資料結構描述集合 S 的一個分割 (partition)，也就是描述一組 S 的子集合，其中任何兩個子集合的交集都是空集合，這一組子集合的聯集是 S，例如下面的 DS1 以及 DS2：

令 S = {0,1, 2, 3, 4, 5, 6, 7}
DS1 = {0}, {1, 2}, {3, 6, 7}, {4}, {5}
DS2 = {0, 1, 2, 5}, {3, 6, 7}, {4}

一個 disjoint-sets 資料結構中每一個子集合都會任意指定一個代表元素, 例如上面每一個子集合中都有一個元素標示為紅色

disjoint-sets 抽象資料型態支援兩個主要的運算方法：

    1. find(i): 找到元素 i 的子集合，回傳該子集合的代表元素
    2. union(i, j): 將包含元素 i 的子集合與包含元素 j 的子集合聯集起來

以上面的 DS1 為例:

  • 執行 find(0) 會得到 0, 執行 find(6) 會得到 7, 同時 find(1)==find(2)

  • 執行 union(1,4) 會使得 DS1 成為 {0, 3, 6, 7}, {1, 2}, {4}, {5}, 其中子集合 {0, 3, 6, 7} 的代表元素需要為這四個元素中的一個, 一般都是原來的兩個子集合 {0} 和 {3, 6, 7} 的代表元素中的一個

  • 執行 union(0,2), 再執行 union(1,5) 會使得 DS1 成為等效於 DS2 的 disjoint-sets (每一個子集合的代表元素不見得和 DS2 一樣)

此外還有一個 makeset() 的運算, 將 disjoint-sets 資料結構初始化為 n 個含有單一元素的子集合, 例如

DS3 = {0}, {1}, {2}, {3}, {4}, {5}, {6}, {7}

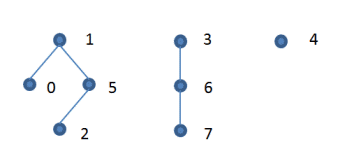
我們可以用 陣列 簡單地實作 「互斥集合」資料結構, 用樹狀架構來代表各個子集合, 例如 DS2 = {0, 1, 2, 5}, {3, 6, 7}, {4} 表示為下圖之三個樹狀架構

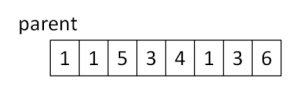
用樹根節點作為這個子集合的代表元素, 下圖的整數陣列中每一個元素 parent[i] 中紀錄的是節點 i 的父節點, 如果是根節點的話 parent[i] 記錄的是 i 自己, 例如 DS2 = {0, 1, 2, 5}, {3, 6, 7}, {4} 以下列整數陣列表示

注意: 用這種表示方法來表示子集合並不是唯一的，同一個子集合可以有不同的樹狀架構，不考慮效率的情況下這個實作可以滿足下列 main() 函式中的基本測試
下面是一個實作 互斥集合 (Disjoint Sets) 的 C 程式 
#include <cstdlib>
#include <cassert>
#include <iostream>
#include <iomanip>
using namespace std;

void makeSets(int nNodes, int parent[]);
int  findSets(int i, int nNodes, const int parent[]);
void mergeTrees(int i, int j, int nNodes, int parent[]);
void unionSets(int i, int j, int nNodes, int parent[]);
int  equalSets(int nNodes1, const int parent1[], int nNodes2, const int parent2[]);
void printSets(int nNodes, const int parent[]);

int main()
{
    const int nNodes=8;
    int parent[nNodes];
    int i;
    const int p1[8] = {0,1,2,3,4,5,6,7};
    const int p2[8] = {0,0,2,3,4,5,6,7};
    const int p3[8] = {0,0,3,3,4,5,6,7};
    const int p4[8] = {0,0,3,3,4,4,6,7};
    const int p5[8] = {0,0,3,3,5,5,5,7};
    const int p6[8] = {0,0,3,3,6,4,6,6};
    const int p7[8] = {0,0,3,4,6,4,6,6};
    const int p8[8] = {7,0,3,4,6,4,6,6};
    makeSets(nNodes, parent);
    assert(equalSets(nNodes, parent, nNodes, p1));
    unionSets(0, 1, nNodes, parent);
    assert(equalSets(nNodes, parent, nNodes, p2));
    unionSets(2, 3, nNodes, parent);
    assert(equalSets(nNodes, parent, nNodes, p3));
    unionSets(4, 5, nNodes, parent);
    assert(equalSets(nNodes, parent, nNodes, p4));
    unionSets(4, 6, nNodes, parent);
    assert(equalSets(nNodes, parent, nNodes, p5));
    unionSets(4, 7, nNodes, parent);
    assert(equalSets(nNodes, parent, nNodes, p6));
    unionSets(3, 7, nNodes, parent);
    assert(equalSets(nNodes, parent, nNodes, p7));
    unionSets(2, 1, nNodes, parent);
    assert(equalSets(nNodes, parent, nNodes, p8));
    printSets(nNodes, parent);
    system("pause");
    return 0;
}

void printSets(int nNodes, const int parent[])
{
    int i, j;
    
    int *printed = (int *) malloc(nNodes*sizeof(int));
    for (i=0; i<nNodes; i++) printed[i] = 0;
    for (i=0; i<nNodes; i++)
        if (!printed[i])
        {
            if (i==0)
                cout << "{";
            else
                cout << ", {";
            cout << i;
            for (j=i+1; j<nNodes; j++)
                if (!printed[j] && 
                    findSets(i, nNodes, parent)==findSets(j, nNodes, parent))
                {
                    cout << ", " << j;
                    printed[j] = 1;
                }
            cout << "}";
        }
    cout << endl;
    free(printed);
}


void makeSets(int nNodes, int parent[])
{
    int i;
    for (i=0; i<nNodes; i++)
        parent[i] = i;
}

int findSets(int i, int nNodes, const int parent[])
{
    if ((i<0)||(i>=nNodes)) return -1;
    if (i == parent[i]) return i;
    return findSets(parent[i], nNodes, parent);
}

void mergeTrees(int i, int j, int nNodes, int parent[])
{
    if ((i<0)||(i>=nNodes)) return;
    if ((j<0)||(j>=nNodes)) return;
    parent[i] = j;
}

void unionSets(int i, int j, int nNodes, int parent[])
{
    if ((i<0)||(i>=nNodes)) return;
    if ((j<0)||(j>=nNodes)) return;
    mergeTrees(findSets(i, nNodes, parent), 
               findSets(j, nNodes, parent),
               nNodes, parent);
}

int equalSets(int nNodes1, const int parent1[], int nNodes2, const int parent2[])
{
    if (nNodes1 != nNodes2) return 0;
    for (int i=0; i<nNodes1; i++)
    {
        if (findSets(findSets(i, nNodes1, parent1), nNodes1, parent2) !=
            findSets(i, nNodes1, parent2))
            return 0;
        if (findSets(findSets(i, nNodes1, parent2), nNodes1, parent1) !=
            findSets(i, nNodes1, parent1))
            return 0;
    }
   return 1;
}

下面是一個實作 互斥集合 (Disjoint Sets) 的 C++ 物件化程式

 

/* DisjointSets.h */

#pragma once

class DisjointSets
{
public:
    DisjointSets(void);
    virtual ~DisjointSets(void);
    void makeSets(int nNodes, const int *parent=0);
    int findSets(int i) const;
    void unionSets(int i, int j);
    int equalSets(const DisjointSets& rhs) const;
    void print();
    static void unitTest(void);
private:
    void mergeTrees(int i, int j);
    int m_nNodes;
    int m_parent[100];
};

/* DisjointSets.cpp */

#include "DisjointSets.h"
#include <cassert>
#include <iostream>
using namespace std;

DisjointSets::DisjointSets(void)
{
}


DisjointSets::~DisjointSets(void)
{
}


void DisjointSets::makeSets(int nNodes, const int *parent)
{
    int i;
    m_nNodes = nNodes;
    if (parent == 0)
        for (i=0; i<nNodes; i++)
            m_parent[i] = i;
    else
        for (i=0; i<nNodes; i++)
            m_parent[i] = parent[i];
}


int DisjointSets::findSets(int i) const
{
    if ((i<0)||(i>=m_nNodes)) return -1;
    if (i == m_parent[i]) return i;
    return findSets(m_parent[i]);
}


void DisjointSets::mergeTrees(int i, int j)
{
    if ((i<0)||(i>=m_nNodes)) return;
    if ((j<0)||(j>=m_nNodes)) return;
    m_parent[i] = j;
}


void DisjointSets::unionSets(int i, int j)
{
    if ((i<0)||(i>=m_nNodes)) return;
    if ((j<0)||(j>=m_nNodes)) return;
    mergeTrees(findSets(i), findSets(j));
}


int DisjointSets::equalSets(const DisjointSets& rhs) const
{
    int i;
    if (m_nNodes != rhs.m_nNodes) return 0;
    for (i=0; i<m_nNodes; i++)
        if ((rhs.findSets(findSets(i)) != rhs.findSets(i)) ||
            (findSets(rhs.findSets(i)) != findSets(i)))
            return 0;
    return 1;
}

void DisjointSets::unitTest(void)
{
    const int nNodes=8;
    int i;
    const int p1[8] = {0,1,2,3,4,5,6,7};
    const int p2[8] = {0,0,2,3,4,5,6,7};
    const int p3[8] = {0,0,3,3,4,5,6,7};
    const int p4[8] = {0,0,3,3,4,4,6,7};
    const int p5[8] = {0,0,3,3,5,5,5,7};
    const int p6[8] = {0,0,3,3,6,4,6,6};
    const int p7[8] = {0,0,3,4,6,4,6,6};
    const int p8[8] = {7,0,3,4,6,4,6,6};
    DisjointSets ds1, ds2;
    ds1.makeSets(nNodes);
    ds2.makeSets(nNodes, p1);
    assert(ds1.equalSets(ds2));

    ds1.unionSets(0, 1);
    ds2.makeSets(nNodes, p2);
    assert(ds1.equalSets(ds2));

    ds1.unionSets(2, 3);
    ds2.makeSets(nNodes, p3);
    assert(ds1.equalSets(ds2));

    ds1.unionSets(4, 5);
    ds2.makeSets(nNodes, p4);
    assert(ds1.equalSets(ds2));

    ds1.unionSets(4, 6);
    ds2.makeSets(nNodes, p5);
    assert(ds1.equalSets(ds2));

    ds1.unionSets(4, 7);
    ds2.makeSets(nNodes, p6);
    assert(ds1.equalSets(ds2));

    ds1.unionSets(3, 7);
    ds2.makeSets(nNodes, p7);
    assert(ds1.equalSets(ds2));

    ds1.unionSets(2, 1);
    ds2.makeSets(nNodes, p8);
    assert(ds1.equalSets(ds2));

    ds1.print();
}

void DisjointSets::print()
{
    int i, j, printed[100];
    for (i=0; i<m_nNodes; i++) printed[i] = 0;
    for (i=0; i<m_nNodes; i++)
        if (!printed[i])
        {
            if (i==0)
                cout << "{";
            else
                cout << ", {";
            cout << i;
            for (j=i+1; j<m_nNodes; j++)
                if (!printed[j] && findSets(i)==findSets(j))
                {
                    cout << ", " << j;
                    printed[j] = 1;
                }
            cout << "}";
        }
    cout << endl;
}

/* main.cpp */

#include "DisjointSets.h"
#include <cstdlib>

int main()
{
    DisjointSets::unitTest();
    system("pause");
    return 0;
}

回 C++ 物件導向程式設計課程 首頁

製作日期: 03/25/2016 by 丁培毅 (Pei-yih Ting)
E-mail: pyting@mail.ntou.edu.tw TEL: 02 24622192x6615
海洋大學 電機資訊學院 資訊工程學系 Lagoon