1042 Quiz#1 互斥集合 (Disjoint Sets)

| C++ 實習測試: 互斥集合 (disjoint-sets) 類別製作 |
| 時間: 60分鐘 (10:20 上傳時間截止) |
| 令集合 S 為整數 0 到 n-1 的集合,「互斥集合 (disjoint-sets)」資料結構 (或稱為「不相交集合」, 也稱為 union-find 資料結構, 或是 merge-find 資料結構) 的定義如下:
|
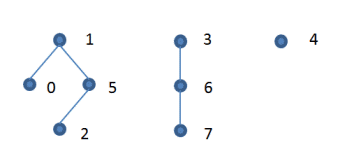
| 我們可以用 陣列 簡單地實作 「互斥集合」資料結構, 用樹狀架構來代表各個子集合, 例如 DS2 = {0, 1, 2, 5}, {3, 6, 7}, {4} 表示為下圖之三個樹狀架構
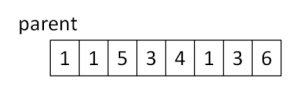
用樹根節點作為這個子集合的代表元素, 下圖的整數陣列中每一個元素 parent[i] 中紀錄的是節點 i 的父節點, 如果是根節點的話 parent[i] 記錄的是 i 自己, 例如 DS2 = {0, 1, 2, 5}, {3, 6, 7}, {4} 以下列整數陣列表示
注意: 用這種表示方法來表示子集合並不是唯一的,同一個子集合可以有不同的樹狀架構,不考慮效率的情況下這個實作可以滿足下列 main() 函式中的基本測試 |
#include <cstdlib>
#include <cassert>
#include <iostream>
#include <iomanip>
using namespace std;
void makeSets(int nNodes, int parent[]);
int findSets(int i, int nNodes, const int parent[]);
void mergeTrees(int i, int j, int nNodes, int parent[]);
void unionSets(int i, int j, int nNodes, int parent[]);
int equalSets(int nNodes1, const int parent1[], int nNodes2, const int parent2[]);
void printSets(int nNodes, const int parent[]);
int main()
{
const int nNodes=8;
int parent[nNodes];
int i;
const int p1[8] = {0,1,2,3,4,5,6,7};
const int p2[8] = {0,0,2,3,4,5,6,7};
const int p3[8] = {0,0,3,3,4,5,6,7};
const int p4[8] = {0,0,3,3,4,4,6,7};
const int p5[8] = {0,0,3,3,5,5,5,7};
const int p6[8] = {0,0,3,3,6,4,6,6};
const int p7[8] = {0,0,3,4,6,4,6,6};
const int p8[8] = {7,0,3,4,6,4,6,6};
makeSets(nNodes, parent);
assert(equalSets(nNodes, parent, nNodes, p1));
unionSets(0, 1, nNodes, parent);
assert(equalSets(nNodes, parent, nNodes, p2));
unionSets(2, 3, nNodes, parent);
assert(equalSets(nNodes, parent, nNodes, p3));
unionSets(4, 5, nNodes, parent);
assert(equalSets(nNodes, parent, nNodes, p4));
unionSets(4, 6, nNodes, parent);
assert(equalSets(nNodes, parent, nNodes, p5));
unionSets(4, 7, nNodes, parent);
assert(equalSets(nNodes, parent, nNodes, p6));
unionSets(3, 7, nNodes, parent);
assert(equalSets(nNodes, parent, nNodes, p7));
unionSets(2, 1, nNodes, parent);
assert(equalSets(nNodes, parent, nNodes, p8));
printSets(nNodes, parent);
system("pause");
return 0;
}
void printSets(int nNodes, const int parent[])
{
int i, j;
int *printed = (int *) malloc(nNodes*sizeof(int));
for (i=0; i<nNodes; i++) printed[i] = 0;
for (i=0; i<nNodes; i++)
if (!printed[i])
{
if (i==0)
cout << "{";
else
cout << ", {";
cout << i;
for (j=i+1; j<nNodes; j++)
if (!printed[j] &&
findSets(i, nNodes, parent)==findSets(j, nNodes, parent))
{
cout << ", " << j;
printed[j] = 1;
}
cout << "}";
}
cout << endl;
free(printed);
}
void makeSets(int nNodes, int parent[])
{
int i;
for (i=0; i<nNodes; i++)
parent[i] = i;
}
int findSets(int i, int nNodes, const int parent[])
{
if ((i<0)||(i>=nNodes)) return -1;
if (i == parent[i]) return i;
return findSets(parent[i], nNodes, parent);
}
void mergeTrees(int i, int j, int nNodes, int parent[])
{
if ((i<0)||(i>=nNodes)) return;
if ((j<0)||(j>=nNodes)) return;
parent[i] = j;
}
void unionSets(int i, int j, int nNodes, int parent[])
{
if ((i<0)||(i>=nNodes)) return;
if ((j<0)||(j>=nNodes)) return;
mergeTrees(findSets(i, nNodes, parent),
findSets(j, nNodes, parent),
nNodes, parent);
}
int equalSets(int nNodes1, const int parent1[], int nNodes2, const int parent2[])
{
// 請實作一個測試兩個 disjoint-sets 是否相等的函式, 相等請回傳 1, 不等請回傳 0
// 首先檢查兩個 disjoint-sets 的元素個數是否相等
// 測試兩個集合 S1 與 S2 是否相等的基本方法是檢查 S1 中的每一個元素是否在 S2 裡,
// 同時反過來檢查 S2 中的每一個元素是否在 S1 裡, 請運用 findSet() 函式來測試,
// 請考慮兩個集合的代表元素可能會不一樣
return 1;
}
|
考試時間: 60分鐘 (10:20 上傳時間截止)
|
| 將所完成的 project (只需保留 .cpp, .h, .sln 以及 .vcxproj 檔案即可; 刪除掉 .suo, .sdf, .filters, .users, debug\ 資料匣, 以及 ipch\ 資料匣下的所有內容) 以 zip/rar/7zip 程式將整個資料匣壓縮起來, 在「考試作業」繳交區選擇 Labtest1上傳 |
後續練習這個 DisjointSets 物件可以用來
演算法大致描述如下: Initialize DisjointSets S with n=nRows*nCols elements and an nRows x nCols maze of '*' except maze[0][0] andthe following 4 cases do not satisfy the "route constraints" |