Lab 9-1: CComplex 的應用與 Mandelbrot 圖形界面

| 實習目標 | 使用實習 3-1,
4-2 中的CComplex 類別 做一個 Mandelbrot 碎形圖形 練習與基本圖形界面的合作 練習視窗界面程式的 debug |
|---|---|
| 步驟一 |
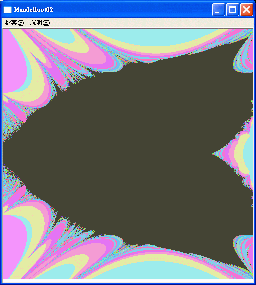
請執行 Mandelbrot02a 程式
這個程式會顯示 Mandelbrot 碎形圖形如下圖: 
這個碎形圖形其實是根據複數平面上每個複數點的一個特別性質畫出來的, 對於任意一個複數 c, 我們可以定義一個複數數列 z0 = 0, zi = (zi-1)2 + c, 如果我們規定複數 zi 的實部或是虛部的絕對值超過 2 就稱為 "發散", 對於每一個複數 c 來說都會有一個 i, 只要大於這個 i, zi就會發散, 如此每一個 c 都有一個對應的 i, 將這些 i 值在視窗中用不同的顏色表示出來就出現上面這張圖, 例如上圖中外圈草綠色部份的那些點所對應的 i 值都是相同的, 可能是 2 或 3 吧。 |
| 步驟二 | 這個程式因為使用視窗的界面, 所以你沒有辦法用 cout, cin 來偵錯, 如果程式不幸出錯或是沒有顯示的話你還是需要一步一步地
debug, 當然你可以用 VC 的 source debugger 一步一步執行來找錯誤, 不過這是最慢的方法, 同時在過程中你也會看到一大堆根本不是你寫的程式...
很困擾呢...
在使用 Microsoft Foundation Class (MFC) 製作視窗界面時, 我們常用一個 TRACE 巨集來取代 cout, TRACE 的用法和 printf 很像, 相信你還沒有忘記怎樣用 printf, 例如:
TRACE("m_data=%d\n", m_data);
TRACE("m_doubleData=%f\n", m_doubleData);
這些敘述的輸出會到哪裡去呢?
如果你用 debug 模式(偵錯/開始偵錯 F5)執行的話, 會跑到 output 視窗中, 如果你是正常執行(偵錯/啟動但不偵錯 Ctrl-F5)的話, 可以開啟 dbwin32 程式來顯示偵錯的結果 |
| 步驟三 |
接下來我們介紹如何一步一步地產生這個碎形圖形, 首先你需要把繪圖區域對應到複數平面, 例如將畫面上 500 x 500 像素 (pixel) 的區域對應到複數平面上 (-1.65, -1.15)-(0.65, 1.15) 的方形區域上, 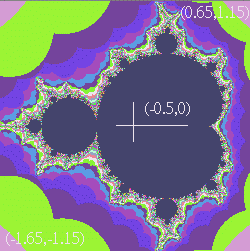
int i, j;
Complex c;
double step = range / (windowSize-1);
for (i=0; i<windowSize; i++)
for (j=0; j<windowSize; j++)
c = Complex(centerX-range/2.0+i*step,
centerY+range/2.0-j*step);
上面迴圈中每一次算出來的複數 c 就是每個座標點 (i, j) 所對應的複數 c 的值。
接下來我們需要測試繪圖區域內每一個點, 看看在下列的測試公式下, 每一個 c 值發散的狀況:
令複數 z 的初始值為 0+0i
令每一個點的複數座標為 c
重複計算
z = z * z + c
每次運算後, 如果 z 的實部或是虛部的絕對值超過 2
的話, 就表示已經發散掉了, 此時請記錄由開始到
發散需要計算上式幾次, 通常在前 50 次計算中,
會發散的點就已經有百分之九十九都發散掉了,
剩下的也幾乎不會發散了
上圖中同一顏色的那些點代表它們都在算到相同次數時發散掉的 (實部或是虛部大於 2 或是小於 -2 的)
上面是一個很漂亮的圖形, 而且如果放大來看的話, 它會不斷重複類似的圖案, 請執行 Mandelbrot03a, 在自然界中這種圖形很多, 這種圖形也常常可以用簡單的數學公式描述出來 如果發散的條件改成 "當 z 的實部和虛部的絕對值都超過 2" 的話, 還是一個碎形圖形, 但是看起來有點醜, 沒有那麼賞心悅目了
如果你等一下子實作時看到像底下這樣子的圖 這是 Complex 的實作出了一點問題 |
| 步驟四 |
請下載圖形界面程式碼 Mandelbrot02b.rar, 解壓縮出來到硬碟中(請不要放在隨身碟裡, 隨身碟的檔案系統是FAT32或是FAT16, vc2008 的圖形介面程式碼需要放在NTFS的檔案系統裡, 才能順利用debug模式編譯測試, 算是 vc2008 的 bug 吧!), 請編譯並且執行, 你應該可以看到顯示的視窗中是全部空白的, 選單中有 檔案/MaxIteration 設定的選項, 這個選項可以讓使用者在操作的時候, 設定判斷一個點是否發散時需要測試的 i 值最大為多少, 我們將在這個 project 中應用你先前寫的 CComplex 類別來撰寫程式, 請下載你先前製作好的 CComplex 類別的程式碼 (請注意, 大家寫的 CComplex 類別基本介面都是一樣的,如果你發現你的 CComplex 物件表現不太對,可以借用別人的來測試比較看看, 這也是物件化的程式一個很重要的好處) |
| 步驟五 | 在類別檢視視窗中你可以找到 Mandelbrot 類別, 打開這個類別你可以看到下列類別的定義以及空的成員函式:
class Mandelbrot
{
public:
Mandelbrot(double centerX, double centerY, double range);
void generateData(int ** &data,
int windowSize,
int maxIterations);
void deleteData(int ** &data, int windowSize);
private:
...
};
你可以在
Mandelbrot::Mandelbrot(double centerX, double centerY, double range)
{
}
函式中加一列敘述 TRACE("Mandelbrot::Mandelbrot() is called\n");, 記得執行 dbwin32,
然後編譯執行這個程式,
看到列印出來的訊息, 你會發現這個建構元函式已經被呼叫過了,
也就是說這個物件已經產生了,
這個 Mandelbrot 類別的物件最主要負責計算每一個複數點希望在螢幕上顯示的 i 值,
用來告訴圖形界面程式該顯示什麼,
圖形界面程式執行起來時會自動建構一個這個類別的物件
傳入建構元函式的參數是繪圖區域中心點的複數座標, 例如 (-0.5, 0), 以及繪圖區域的寬與高 (目前所畫的是一個方形區域), 例如 2.3, (你可以用 TRACE 敘述看一下), 傳進來的資料請在 Mandelbrot 類別中設計資料成員記錄下來 |
| 步驟六 |
接下來我們看到 generateData() 這個成員函式,
圖形介面程式每次需要計算整個平面的複數對應的 i 值時就會呼叫它,
它應該要配置如下圖的資料陣列, 計算每個點的 i 值,
並且將陣列的記憶體起始位址放在 data 變數內:
void generateData(int ** &data, int windowSize, int maxIterations); 這個成員函式應該要檢查傳入的指標, 如果是 0 的話, 動態配置一塊二維的整數 (int) 陣列, 其架構如下圖 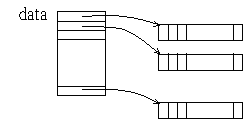
記得修改後先把配置好的陣列每一個元素設成定值 (例如 data[i][j] = 10; 然後編譯和測試 |
| 步驟七 |
這個 data 陣列的每一個元素代表繪圖區域中一個像素 (pixel),
依照一般的慣例,
data[0][0] 代表視窗的左上角, data[0][windowSize-1] 代表右上角,
data[windowSize-1][0] 代表左下角, data[windowSize-1][windowSize-1] 代表右下角,
你需要計算那個點的複數座標,
依照步驟三中的公式算算看在做到第幾次時 z 的實部或是虛部的絕對值超過 2,
然後記錄在 data[i][j] 中,
請注意傳入的 maxIterations 數值是你在測試時的最大次數
在你真正去算 z 的運算式並且算出 data[i][j] 之前, 你可以先把 data[i][j] 設定成一些簡單的圖樣來測試一下, 例如 (直紋):
for (i=0; i<windowSize; i++)
for (j=0; j<windowSize; j++)
data[i][j] = i%256;
或是 (矩形)
int i, j, min_i, min_j;
for (i=0; i<windowSize; i++)
for (j=0; j<windowSize; j++)
{
min_i = i<(windowSize-i) ? i : windowSize-i;
min_j = j<(windowSize-j) ? j : windowSize-j;
data[i][j] = min_i<min_j ? min_i : min_j;
}
請注意 data[i][j] 的數值一定要維持在 [0, 255] 間,否則繪圖程式會當掉 (這是這個繪圖程式和你之間定義的介面) |
| 步驟八 | 上面計算步驟中你需要用到 CComplex 的複數類別, 同時類別中要提供
CComplex add(const CComplex &rhs) const;
CComplex multiply(const CComplex &rhs) const;
兩個成員函式, 這兩個成員函式我們在前面的實習中定義過類似的東西, 不過那時定義的是 add(const CComplex &rhs) 實際上應該叫做
addEqual(const CComplex &rhs), 也就是把 rhs 的複數物件和自己這個物件加起來, 並且修改自己這個物件的內容,
你可以直接用上次寫的成員函式來實作 z = z * z + c, 程式碼看起來如下
z.multiplyEqual(z);
z.addEqual(c)
你也可以修改你的函式 addEqual() 為沒有 side effect 的 add(),
讓它在把兩個複數加起來以後,
不要修改自己那個物件,
而是以傳值 (call by value) 的方式把一個 CComplex
的物件傳回,
如此你在實作 z = z * z + c 時可以用類似下列的敘述:
z = c.add(z.multiply(z));
或是
tmp = z.multiply(z);
z = tmp.add(c);
請注意如果你直接將前面實習的 Complex.cpp 和 Complex.h 拷貝進來的話, 請在你的 Complex.cpp 檔案的第一列加入
#include "stdafx.h" 如此 compiler 才不會跟你抱怨說它找不到
pch (precompile header) 檔案 |
| 步驟九 |
void deleteData(int ** &data, int windowSize);
函式中需要實作將步驟六中配置的二維陣列刪除的程式碼 一切順利的話你的執行畫面上應該可以看到 Mandelbrot 的顯示了 |
| 步驟十 | 請測試一下選單 檔案/MaxIterations 設定, 當使用者更改過這個設定值 (10-120) 後, 你提供的
generateData 會重新被呼叫到, (你可以用 TRACE 敘述驗證這件事) 同時 maxIterations 參數會有新的數值傳入
由於你在這個程式中有動態配置記憶體, 請特別在 dbwin32 視窗中確定一下程式結束時有沒有 memory leakage (請注意, 你不需要使用先前介紹的 memory_leak.h memory_leak.cpp , 使用MFC dll 的程式自動會把記憶體遺漏的訊息顯示在 dbwin32 視窗中, 你可以試著配置一小塊記憶體, 程式結束前不要刪除, 看看是否會偵測的到) |
| 步驟十一 | 請助教檢查後, 將所完成的 project (去掉 debug/ 資料匣下的所有內容) 壓縮起來, 選擇 Lab9-1 上傳, 後面的實習課程可能需要使用這裡所完成的程式 |